
分析 分两种情况进行讨论:(1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出;
(2)当△ABC为钝角三角形时,求出BC的长,从而可将△ABC的周长求出.
解答 32cm或42cm解:分两种情况说明: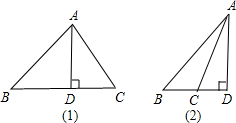
(1)当△ABC为锐角三角形时,在Rt△ABD中,
BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
在Rt△ACD中,
CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{1{5}^{2}-1{2}^{2}}$=9,
∴BC=5+9=14,
∴△ABC的周长为:15+13+14=42(cm);
(2)当△ABC为钝角三角形时,
BC=BD-CD=9-5=4.
∴△ABC的周长为:15+13+4=32(cm);
故答案为:42cm或32cm.
点评 此题考查了勾股定理及解直角三角形的知识,在解本题时应分两种情况进行讨论,易错点在于漏解,同学们思考问题一定要全面,有一定难度.


科目:初中数学 来源: 题型:解答题
 如图所示,一只蚂蚁从O点出发,沿北偏东60°方向爬行1.1cm,碰到一障碍物B后,又沿西北方向爬行1.6cm到C处.
如图所示,一只蚂蚁从O点出发,沿北偏东60°方向爬行1.1cm,碰到一障碍物B后,又沿西北方向爬行1.6cm到C处.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
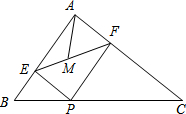 如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P为边BC上一动点(P不与B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是$\frac{30}{13}$≤AM<6.
如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P为边BC上一动点(P不与B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是$\frac{30}{13}$≤AM<6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com