
 ��ͼ��AB�ǡ�O��һ���ң�ֱ��CD��AB��E������CA��CB����M��N�ֱ�ΪCA��CB���е㣬����ME��NE��
��ͼ��AB�ǡ�O��һ���ң�ֱ��CD��AB��E������CA��CB����M��N�ֱ�ΪCA��CB���е㣬����ME��NE������ ��1������֤���ı���CMEN��ƽ���ı��Σ���֤��EM=EN���ɣ�
��2���ٵ���MCN=90��ʱ���ı���CMEN�������Σ���ʱAB��ֱ������E��O�غϣ��ɴ˼��ɽ�����⣮
�ڷ�����������⣬����ACB=60�㣬��ͼ1�У�����OA����RT��AOE�У�����OE=$\frac{1}{2}$OA=2�����ɽ�����⣬����CME=60��ʱ�����ACB=120�㣬֤����ACO�ǵȱ������Σ����ɽ�����⣮
��3������S����CMEN=$\frac{1}{2}$MN•EC�����NM���ɽ�����⣮
��� �⣺��1�����ۣ��ı���CMEN�����Σ�
���ɣ���ֱ��CD��AB��E��
��AE=EB��CA=CB��
��AM=CM��CN=NB��
��EM��BC��EN��AC��EM=$\frac{1}{2}$BC��EN=$\frac{1}{2}$AC��
��EM=EN��
���ı���CMEN��ƽ���ı��Σ�
��EM=EN��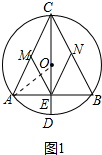
���ı���CMEN�����Σ�
��2���ٵ���MCN=90��ʱ���ı���CMEN�������Σ�
��AB��ֱ������E��O�غϣ�
��CE=CO=4��
�ڵ���ACB=60�㣬��ͼ1�У�����OA����RT��AOE�У��ߡ�AEO=90�㣬��OAE=30�㣬OA=4��
��OE=$\frac{1}{2}$OA=2��
��CE=OC+OE=5��
����CME=60��ʱ�����ACB=120�㣬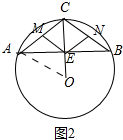 ��ͼ2�У�����OA��
��ͼ2�У�����OA��
���ACO=��BCO=60�㣬
���ACO�ǵȱ������Σ�
��AE��OC��
��CE=EO=2��
�൱xΪ5��2ʱ���ı���CMEN����һ������60�㣮
��3�����ı���CMEN�����Σ�
��S����CMEN=$\frac{1}{2}$MN•EC��
��MN=$\frac{1}{2}$AB=AE=$\sqrt{{4}^{2}-��x-4��^{2}}$=$\sqrt{8x-{x}^{2}}$��
��S����CMEN=$\frac{1}{2}$MN•EC=$\frac{1}{2}$•$\sqrt{8x-{x}^{2}}$•x=$\frac{x•\sqrt{8x-{x}^{2}}}{2}$����0��x��8����
���� ���⿼��Բ�ۺ��⡢�ȱ������ε����ʡ������ε����ʴ���������֪ʶ������Ĺؼ������Ӧ����Щ֪ʶ������⣬ѧ��������ۣ�����©�⣬�����п�ѹ���⣮


 ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ����ͬѧϲ����ˮ������ͼ������������3�·��������ˮ�����Ƶ�����ͳ��ͼ������������8kg�������õ��������ƻ�����ˣ�������
����ͬѧϲ����ˮ������ͼ������������3�·��������ˮ�����Ƶ�����ͳ��ͼ������������8kg�������õ��������ƻ�����ˣ�������| A�� | 5kg | B�� | 6kg | C�� | 7kg | D�� | 8kg |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ���ھ���ABCD�У�AB=6cm��BC=8cm���Խ���AC��BD���ڵ�O����E�ӵ�A��������AD���������˶����ٶ�Ϊ1cm/s��ͬʱ����F�ӵ�C��������CD���������˶����ٶ�Ϊ1cm/s����һ����ֹͣ�˶�ʱ����һ����Ҳֹͣ�˶�������EO���ӳ�����BC�ڵ�G�������˶�ʱ��Ϊt��s����0��t��6��������������⣺
��֪����ͼ���ھ���ABCD�У�AB=6cm��BC=8cm���Խ���AC��BD���ڵ�O����E�ӵ�A��������AD���������˶����ٶ�Ϊ1cm/s��ͬʱ����F�ӵ�C��������CD���������˶����ٶ�Ϊ1cm/s����һ����ֹͣ�˶�ʱ����һ����Ҳֹͣ�˶�������EO���ӳ�����BC�ڵ�G�������˶�ʱ��Ϊt��s����0��t��6��������������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com