
【题目】如图,平行四边形ABCD,DE交BC于F,交AB的延长线于E,且∠EDB=∠C.
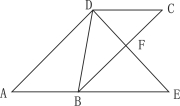
(1)求证:△ADE∽△DBE;
(2)若DE=9cm,AE=12cm,求DC的长.
科目:初中数学 来源: 题型:
【题目】某地上年度电价为0.8元/度,年用电量为1亿度,本年度计划将电价调至0.55~0.75元/度之间,经测算,若电价调至x元/度,则本年度新增用电量y(亿度)与(x-0.4)成反比例.又知当x=0.65时,y=0.8.
(1)求y与x之间的函数解析式;
(2)若每度电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年度增加20%?[收益=用电量×(实际电价-成本价)]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4,2)、B(n,-4)是一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
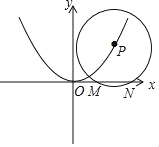
【题目】如图,⊙P的圆心P(m,n)在抛物线y=![]() 上.
上.
(1)写出m与n之间的关系式;
(2)当⊙P与两坐标轴都相切时,求出⊙P的半径;
(3)若⊙P的半径是8,且它在x轴上截得的弦MN,满足0≤MN≤2![]() 时,求出m、n的范围.
时,求出m、n的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m+n=7,点A(m,n)在一个反比例函数的图象上,点A与坐标原点的距离为5,现将这个反比例函数图象绕原点顺时针旋转90o,得到一个新的反比例函数图象,则这个新的反比例函数的解析式是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题提出)
“不以规矩,不能成方圆.”——孟子;“圆,一中同长也.”——墨经.
(1)圆,一中同长也.”体现了古代先哲对“圆”定义的思考,请用现代文翻译:____.
(初步思考)
圆规是我们初中几何学习不可或缺的工具,用圆规不仅可以画圆、画弧,还可以画弧与弧的交点,利用这一特征可以构造很多图形,如:
(2)角平分线:如图1,只用圆规在∠AOB中画出一点P使得点P在∠AOB的角平分线上;对称点:如图2,只用圆规画出点P关于直线l的对称点Q,并说明理由.
 (操作与应用)
(操作与应用)
(3)已知点A、直线l.在图3中只用圆规在直线l上画出两点B、C,使得A、B、C恰好是等腰三角形的3个顶点,(画出一个并写出相等线段即可):
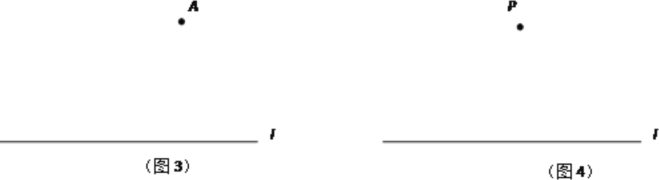
已知点P、直线l.在图4中只用圆规画出一点Q,使得点P、Q所在的直线与直线l平行.(提示:平行四边形对边平行).
(4)已知点O、A、B,只用圆规画出半径为AB的⊙O与点A、B所在直线的交点C、D.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com