
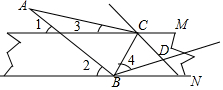
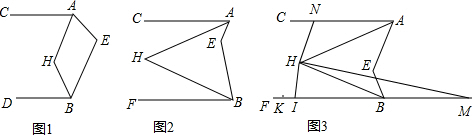
 如图,一两边平行的纸条,将一直角三角板的直角顶点B放在纸片的一条边上,将三角板的另一个角的顶点C放在纸片的另一边上,∠ABC=90°,∠A=30°.
如图,一两边平行的纸条,将一直角三角板的直角顶点B放在纸片的一条边上,将三角板的另一个角的顶点C放在纸片的另一边上,∠ABC=90°,∠A=30°.分析 (1)根据平行线的性质得到∠1=∠2,根据平角的性质即可得到结论;
(2)根据三角形外角的性质即可得到结论;
(3)由已知条件得到2∠MCB=3∠DCB,根据平行线的性质得到∠MCB+∠NBC=180°,于是得到∠CDB=180°-120°=60°,即可得到结论.
解答 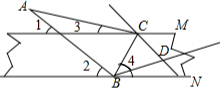 解:(1)∵纸条的边平行,
解:(1)∵纸条的边平行,
∴∠1=∠2,
∵∠ACB=90°,
∴∠2+∠4=90°,
∴∠1+∠4=90°;
(2)∵∠1=∠3+∠A,
∴∠1-∠3=∠A=30°,
∴∠2-∠3=30°;
(3)∵∠MCB=3∠MCD,
∴2∠MCB=3∠DCB,
∵纸条的边平行,
∴∠MCB+∠NBC=180°,
∴$\frac{3}{2}$∠DCB+$\frac{3}{2}$∠DBC=180°,
∴∠MCD+∠DBC=120°,
∴∠CDB=180°-120°=60°,
∴BD与CD不垂直,
点评 本题考查了平行线的性质,三角形的内角和,三角形的外角的性质,熟练掌握平行线的性质是解题的关键.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:填空题
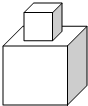 如图所示的某种玩具是由两个正方体用胶水粘合而成的,它们的棱长分别为1米和3 米,为了美观,现要在其表面喷涂油漆,已知喷涂1平方米需用油漆30克,那么喷涂这个玩具共需油漆1740克.
如图所示的某种玩具是由两个正方体用胶水粘合而成的,它们的棱长分别为1米和3 米,为了美观,现要在其表面喷涂油漆,已知喷涂1平方米需用油漆30克,那么喷涂这个玩具共需油漆1740克.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| ∠AOB内射线的条数 | 1 | 2 | 3 | 4 |
| 角的总个数 | 3 | 6 | 10 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
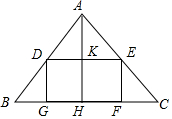 如图,在△ABC中,AH⊥BC于H,BC=12,AH=8,D、E分别为AB、AC上的点,G、F是BC上的两点,四边形DEFG是矩形,设EF=X.
如图,在△ABC中,AH⊥BC于H,BC=12,AH=8,D、E分别为AB、AC上的点,G、F是BC上的两点,四边形DEFG是矩形,设EF=X.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com