

 就可以求出结论;
就可以求出结论;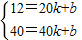 ,
, ,
, t-16.
t-16. 的运用,待定系数法求函数的解析式的运用,在解答此类函数试题时弄清题意和图象的含义是关键.
的运用,待定系数法求函数的解析式的运用,在解答此类函数试题时弄清题意和图象的含义是关键. 

科目:初中数学 来源: 题型:
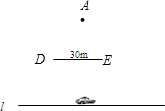 综合实践活动课,某数学兴趣小组在学校操场上想测量汽车的速度,利用如下方法:如图,小王站在点处A(点A处)和公路(l)之间竖立着一块30m长且平行于公路的巨型广告牌(DE).广告牌挡住了小王的视线,请在图中画出视点A的盲区,并将盲区内的那段公路记为BC.已知一辆匀速行驶的汽车经过公路BC段的时间是3s,已知小王到广告牌和公路的距离是分别是40m和80m,求该汽车的速度?
综合实践活动课,某数学兴趣小组在学校操场上想测量汽车的速度,利用如下方法:如图,小王站在点处A(点A处)和公路(l)之间竖立着一块30m长且平行于公路的巨型广告牌(DE).广告牌挡住了小王的视线,请在图中画出视点A的盲区,并将盲区内的那段公路记为BC.已知一辆匀速行驶的汽车经过公路BC段的时间是3s,已知小王到广告牌和公路的距离是分别是40m和80m,求该汽车的速度?查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 2 |
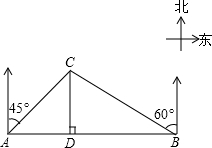
查看答案和解析>>
科目:初中数学 来源: 题型:
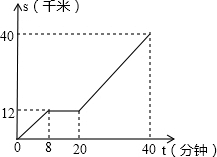 如图,是某汽车在公路上行驶的路程s(千米)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列各题.
如图,是某汽车在公路上行驶的路程s(千米)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列各题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是某汽车在公路上行驶的路程s(千米)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列各题.
如图,是某汽车在公路上行驶的路程s(千米)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列各题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com