
分析 (1)根据开口方向确定a的正负,再根据对称轴的位置确定b的值,根据y1=ax2+bx+c(a≠0)的图象过点(0,1),得到c=1,由此即可判断.
(2)根据题意一次函数y2=ax+b的图象经过点(1,-$\frac{1}{2}$),二次函数y1=ax2+bx+c(a≠0)的对称轴是y轴,由此即可解决问题.
(3)根据题意可知y3=2x+1,y4=mx-1,根据题意即可解决问题.
解答 解:(1)由题意抛物线的对称轴在y轴的值右侧或y轴,开口向下,
∴a<0,-$\frac{b}{2a}$≥0,
∴b≥0,
∵y1=ax2+bx+c(a≠0)的图象过点(0,1),
∴c=1>0,
∴a<0,b≥0,c>0,
故答案为<,≥,>.
(2)∵y2=ax+b,当-1≤x≤1时,y2的最小值为-$\frac{1}{2}$,
∴x=1时,y=-$\frac{1}{2}$,即a+b=-$\frac{1}{2}$,
∵y1≤1,
∴(0,1)是抛物线的顶点,
∴对称轴是y轴,
∴b=0,
∴a=-$\frac{1}{2}$,c=1,
∴y2关于x的函数解析式为y=-$\frac{1}{2}$x2+1.
(3)∵二次函数y1=ax2+bx+c的图象与x轴的一个交点为(-1,0),
∴a-b+1=0,
∴b-a=1,a+1=b,∵c=1,a≠0,
∴y3=2x+1,y4=mx-1,
∵直线y3=2x+1与直线y4=mx-1的图象在第一象限内没有交点,
∴m<0或0<m≤2.
点评 本题考查二次函数综合题、一次函数的性质、待定系数法等知识,解题的关键是灵活应用二次函数或一次函数的性质解决问题,学会利用函数图象解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
 为了促进节能减排,促进节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了三个档次每户每月电费y(元)与用电量x(度)间的函数关系,在每月用电量超过230度时,每多用1度电要比第一档多付电费m元,且此时每户每月电费y(元)与用电量x(度)间的函数关系y=kx-64.5,则m=0.17.
为了促进节能减排,促进节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了三个档次每户每月电费y(元)与用电量x(度)间的函数关系,在每月用电量超过230度时,每多用1度电要比第一档多付电费m元,且此时每户每月电费y(元)与用电量x(度)间的函数关系y=kx-64.5,则m=0.17.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k=1,b=1 | B. | k=0,b=2 | C. | k=-1,b=1 | D. | k=1,b=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4+10+8 | B. | -4+(-10)+(-8) | C. | 4-(+10)-(+8) | D. | 4+(-10)+(-8) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
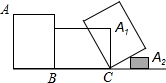 如图,长方形木板的长为4cm,宽为3cm,某同学使之在桌面上做无滑动的翻滚(顺时针方向),木板上点A的位置变化为A→Al→A2,其中第二次翻滚被桌面上的一块小木板挡住,使木板与桌面成30°,则点A滚到A2位置时走过的路径总长为( )
如图,长方形木板的长为4cm,宽为3cm,某同学使之在桌面上做无滑动的翻滚(顺时针方向),木板上点A的位置变化为A→Al→A2,其中第二次翻滚被桌面上的一块小木板挡住,使木板与桌面成30°,则点A滚到A2位置时走过的路径总长为( )| A. | 10cm | B. | 3.5π cm | C. | 4.5π cm | D. | 2.5π cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com