
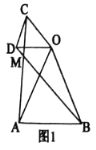
【题目】(1)问题发现:
如图1,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() .
.
填空:①![]() 的值为 ;②
的值为 ;②![]() 的度数为 .
的度数为 .
(2)类比探究:如图2,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请求出
.请求出![]() 的值及
的值及![]() 的度数,并说明理由;
的度数,并说明理由;
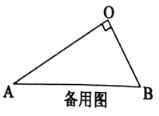
(3)拓展延伸:在(2)的条件下,将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 、
、![]() 所在直线交于点
所在直线交于点![]() ,若
,若![]() ,
,![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 重合时
重合时![]() 的长.
的长.

【答案】(1)①1;②40°;(2)![]() ,∠AMB=90°,理由见详解;(3)AC的长为
,∠AMB=90°,理由见详解;(3)AC的长为![]() 或
或![]() .
.
【解析】
(1)①证明△COA≌△DOB(SAS),得AC=BD,比值为1;
②由△COA≌△DOB,得∠CAO=∠DBO,根据三角形的内角和定理得:∠AMB=180°-(∠DBO+∠OAB+∠ABD)=40°;
(2)根据两边的比相等且夹角相等可得△AOC∽△BOD,则![]() ,由全等三角形的性质得∠AMB的度数;
,由全等三角形的性质得∠AMB的度数;
(3)正确画图形,当点C与点M重合时,有两种情况:如图3和4,同理可得:△AOC∽△BOD,则∠AMB=90°,![]() ,可得AC的长.
,可得AC的长.
解:(1)问题发现
①如图1,
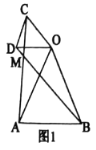
∵∠AOB=∠COD=40°,
∴∠COA=∠DOB,
∵OC=OD,OA=OB,
∴△COA≌△DOB(SAS),
∴AC=BD,
∴![]() ,
,
②∵△COA≌△DOB,
∴∠CAO=∠DBO,
∵∠AOB=40°,
∴∠OAB+∠ABO=140°,
在△AMB中,
∠AMB=180°-(∠CAO+∠OAB+∠ABD)
=180°-(∠DBO+∠OAB+∠ABD)
=180°-140°=40°;
故答案为:①1;②40°;
(2)类比探究
如图2,
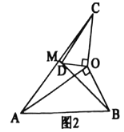
![]() ,∠AMB=90°;
,∠AMB=90°;
理由是:Rt△COD中,∠DCO=30°,∠DOC=90°,
∴![]() ,
,
同理得:![]() ,
,
∴![]() ,
,
∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
∴△AOC∽△BOD,
∴![]() ,∠CAO=∠DBO,
,∠CAO=∠DBO,
在△AMB中,∠AMB=180°-(∠MAB+∠ABM)=180°-(∠OAB+∠ABM+∠DBO)=90°;
(3)拓展延伸
①点C与点M重合时,如图3,同理得:△AOC∽△BOD,
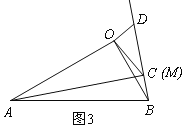
∴∠AMB=90°,![]() ,
,
设BD=x,则AC=![]() ,
,
Rt△COD中,∠OCD=30°,OD=1,
∴CD=2,BC=x-2,
Rt△AOB中,∠OAB=30°,OB=![]() ,
,
∴AB=2OB=![]() ,
,
在Rt△AMB中,由勾股定理得:AC2+BC2=AB2,
![]() ,
,
∴x2-x-6=0,
∴(x-3)(x+2)=0,
∴x1=3,x2=-2,
∴AC=![]() ;
;
②点C与点M重合时,如图4,同理得:∠AMB=90°,![]() ,
,
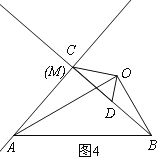
设BD=x,则AC=![]() ,
,
在Rt△AMB中,由勾股定理得:AC2+BC2=AB2,
![]()
∴x2+x-6=0,
∴(x+3)(x-2)=0,
∴x1=-3,x2=2,
∴AC=![]() ;
;
综上所述,AC的长为![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图乙,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
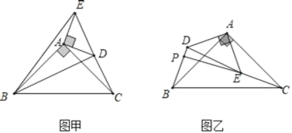
(1)如图甲,将△ADE绕点A旋转,当C、D、E在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是哪几个 .(回答直接写序号)
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2)
(2)若AB=6,AD=3,把△ADE绕点A旋转:
①当∠CAE=90°时,求PB的长;
②直接写出旋转过程中线段PB长的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
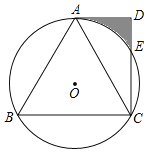
【题目】如图,⊙O为等边△ABC的外接圆,AD∥BC,∠ADC=90°,CD交⊙O于点E.
(1)求证:AD是⊙O的切线;
(2)若DE=2,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
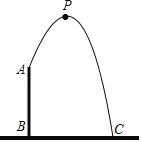
【题目】为庆祝新中国成立70周年,国庆期间,北京举办“普天同庆共筑中国梦”的游园活动,为此,某公园在中央广场处建了一个人工喷泉,如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2m,喷出水流的运动路线是抛物线.如果水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为3.6m,求水流的落地点C到水枪底部B的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一放假期间,甲、乙、丙三位同学到某影城看电影,影城有A,B两部不同电影,甲、乙、丙3人分别从中任选一部观看,每部被选中的可能性相同.
(1)甲同学选择“A部电影”的概率为 ;
(2)用画树状图的方法求甲、乙、丙3人选择同一部电影的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进垃圾分类,推动绿色发展,某工厂购进甲、乙两种型号的机器人用来进行垃圾分类,甲型机器人比乙型机器人每小时多分20kg,甲型机器人分类800kg垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等。
(1)两种机器人每小时分别分类多少垃圾?
(2)现在两种机器人共同分类700kg垃圾,工作2小时后甲型机器人因机器维修退出,求甲型机器人退出后乙型机器人还需工作多长时间才能完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
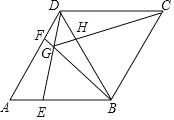
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别是线段AB、AD上的动点(不与端点重合),且AE=DF,BF与DE相交于点G.给出如下几个结论:①△AED≌△DFB;②∠BGE大小会发生变化;③CG平分∠BGD;④若AF=2DF,则BG=6GF;![]() .其中正确的结论有_____(填序号).
.其中正确的结论有_____(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com