
科目: 来源: 题型:

查看答案和解析>>
科目: 来源: 题型:
 名选手进行复赛,成绩见“复赛成绩统计表”.(采用
名选手进行复赛,成绩见“复赛成绩统计表”.(采用 分制,得分都为
分制,得分都为 分以上的整数.)
分以上的整数.)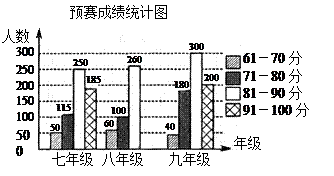 | ||
 | ||
 分以上的人数”对应的圆心角度数是___________.
分以上的人数”对应的圆心角度数是___________. 分以上的人数是预赛时同类成绩人数的
分以上的人数是预赛时同类成绩人数的 ,请补全预赛成绩统计图.
,请补全预赛成绩统计图.查看答案和解析>>
科目: 来源: 题型:
 B
B 的位置(B
的位置(B 在m上),最后沿射线B
在m上),最后沿射线B 的方向平移到△
的方向平移到△

 的位置,其平移距离为线段AC的长度(此时,
的位置,其平移距离为线段AC的长度(此时,
 恰好靠在墙边).
恰好靠在墙边).
查看答案和解析>>
科目: 来源: 题型:
 (2)如图2,若EF=
(2)如图2,若EF= CD,GD=
CD,GD= AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出α.
AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出α. 查看答案和解析>>
科目: 来源: 题型:
 与直线
与直线 及过N点垂直于x轴的直线交于点D.点P(m,0)是x轴上一动点,过点P作y轴的平行线,交射线OM与点E.设以M、E、H、N为顶点的四边形的面积为S.
及过N点垂直于x轴的直线交于点D.点P(m,0)是x轴上一动点,过点P作y轴的平行线,交射线OM与点E.设以M、E、H、N为顶点的四边形的面积为S.
 (4)如图2,设直线PE交射线OD于R,交抛物线C于点Q,
(4)如图2,设直线PE交射线OD于R,交抛物线C于点Q, ,
, 直接写出矩形RQFG与等腰直角三角形OMN重叠部分为
直接写出矩形RQFG与等腰直角三角形OMN重叠部分为查看答案和解析>>
科目: 来源: 题型:


 的奇偶性与单调性;
的奇偶性与单调性; 的解集为
的解集为 的值;
的值; 的反函数为
的反函数为 ,若关于
,若关于 的不等式
的不等式 R)有解,求
R)有解,求 的取值范围.
的取值范围.查看答案和解析>>
科目: 来源: 题型:
 有最小正周期4,且
有最小正周期4,且 时,
时,
 在
在 上的单调性,并求
上的单调性,并求 在
在 上的解析式;
上的解析式; 为何值时,关于
为何值时,关于 的方程
的方程 在
在 上有实数解?
上有实数解?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com