
科目: 来源: 题型:
如果定义:“到三角形的两个顶点距离相等的点,叫做此三角形的准外心.”例如:如图1所示,若PC=PB,则称点P为△ABC的![]() 准外心。 (2+4+6=12分)
准外心。 (2+4+6=12分)
(1) 观察并思考,△ABC的准外心有__________个.
(2) 如图2,△ABC是等边三角形,CD⊥AB,准外![]() 心点 P在高CD上,且PD=
心点 P在高CD上,且PD=![]() ,在图中画出点P点,求∠APB的度数.
,在图中画出点P点,求∠APB的度数.
(3) 已知△ABC为直角三角形,斜边BC=5,AB=3,准外心.P在AC边上,在图中画出P点,并求PA的长.

查看答案和解析>>
科目: 来源: 题型:
因为![]() ,即
,即![]() ,所以
,所以![]() 的整数部分为2,小数部
的整数部分为2,小数部![]() 分为
分为![]() .
.
(10分)
(1) 如果![]() 的整数部分为
的整数部分为![]() ,那
,那![]() = .如果
= .如果![]() ,其中
,其中![]() 是整数,且
是整数,且![]() ,那么
,那么![]() = ,
= , ![]() = . (每空2分)
= . (每空2分)
(2) 将(1)中的![]() 、
、![]() 作为直角三角形的两条边长,请你计算第三边的长度. (4分)
作为直角三角形的两条边长,请你计算第三边的长度. (4分)
查看答案和解析>>
科目: 来源: 题型:
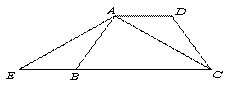
如图,在梯![]() 形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC. (8分)
形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC. (8分)
⑴ 求证:△ABE≌△CDA;
⑵ 若∠DAC=30°,求∠EAC的度数.
查看答案和解析>>
科目: 来源: 题型:
如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上. (3+3+4=10分)
(1) 在图中画出与△ABC关于直线![]() 成轴对称的△A
成轴对称的△A![]() ;
;
(2) 线段![]() 被直线
被直线![]() ;
;
(![]() 3) 在直线
3) 在直线![]() 上找一点P,使PB+PC的长最短,并算出这个最短长度。
上找一点P,使PB+PC的长最短,并算出这个最短长度。
 |
查看答案和解析>>
科目: 来源: 题型:
当遇到梯形问题时,常用分割的方法,将其转化成我们熟悉的图形来解决.(3+3+4=10分)
(1) 按要求分割下列梯形(分割线用虚线)
①将图(1)分割成一个平行四边形和一个三角形
②将图(2)分割成一个长方形和两个直角三角形
 | |||
 | |||
图(1) 图(2)
(2) 如图(3),已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=6,BC=16,CD=10, 请你用适当的方法对梯形进行分割,利用分割后的图形求AD的长.
 |
图(3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com