
科目: 来源: 题型:
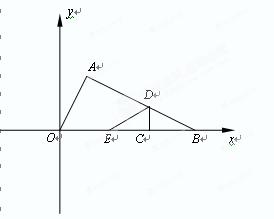
如图在Rt△AOB 中,∠BAO=90°,O为坐标原点,B在x轴正半轴上,A在第一象限,OA和AB的长是方程![]() 两根,且OA<AB.
两根,且OA<AB.
(1)求直线AB的解析式;
(2)将△AOB沿垂直于x轴的线段CD折叠(点C在x轴上,且不与点B重合,点D在线段AB上),使点B落在x轴上,对应点为E,是否存在这样的点C,使得△AED为直角三角形?若存在,求出点C的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=![]() ,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原.
,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原.
(1)当![]() 时,折痕EF的长为 ;
时,折痕EF的长为 ;
当点E与点A重合时,折痕EF的长为 ![]() ;
;
(2)试探索使四边形EPFD为菱形时![]() 的取值范围,请简要说明探索过程。
的取值范围,请简要说明探索过程。
并求当![]() 时,菱形EPFD的边长.
时,菱形EPFD的边长.

查看答案和解析>>
科目: 来源: 题型:
利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理)。当每吨售价为260元时,月销售量为45吨。该经销店为提高经营利润,准备采取降价的方式进行促销。经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨。综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元。
(1)当每吨售价是240元时,计算此时的月销售量;
(2)在遵循“薄利多销”的原则下,问每吨材料售价为多少时,该经销店的月利润为9000元。
查看答案和解析>>
科目: 来源: 题型:
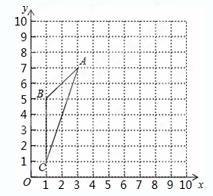
如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.
(1)画出将△ABC向右平移3个单位,再向上平移1个单位所得的△A′B′C′;(友情提醒:对应点的字母不要标错!)
(2)建立如图的直角坐标系,请标出△A′B′C′的外接圆的圆心P的位置,并写出圆心P的坐标:P( , );
(3)将△ABC绕BC旋转一周,求所得几何体的全面积.(结果保留π)
查看答案和解析>>
科目: 来源: 题型:
市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | |
| 甲 | 10 | 9 | 8 | 8 | 10 | 9 |
| 乙 | 10 | 10 | 8 | 10 | 7 | 9 |
(1)根据表格中的数据,分别计算出甲、乙两人的平均成绩;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、![]() (2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com