若，则代数式的值为(      )

A．         B．         C．         D．

在下列四个汽车标志图案中，是中心对称图形的是（　　）

     A．   B．     C．     D．

若在实数范围内有意义，则x的取值范围是（　　）

A．x＜3            B．x≤3            C．x＞3            D．x≥3

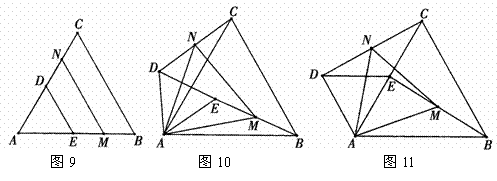
 如图9，若△ABC和△ADE为等边三角形，M，N分别EB，CD的中点，易证：CD=BE，△AMN是等边三角形．

   （1）当把△ADE绕A点旋转到图10的位置时，CD=BE是否仍然成立？若成立请证明，若不成立请说明理由；

   （2）当△ADE绕A点旋转到图11的位置时，△AMN是否还是等边三角形？若是，请给出证明，并求出当AB=2AD时，△ADE与△ABC及△AMN的面积之比；若不是，请说明理由．

已知：m、n是方程x²－6x+5＝0的两个实数根，且m＜n，抛物线y＝－x²+bx+c的图像经过点A(m，0)、B(0，n).

（1）求这个抛物线的解析式；

（2）设（1）中抛物线与轴的另一交点为C，抛物线的顶点为D，试求出点C、D的坐标和△BCD的面积

（3）P是线段OC上的一点，过点P作PH⊥x轴，与抛物线交于H点，若直线BC把△PCH分成面积之比为2∶3的两部分，请求出P点的坐标.

如图，已知∠=90°，线段AB=10，若点A在上滑动，点B随着线段AB在射线 上滑动，（A、B与O不重合），Rt△AOB的内切⊙K分别与OA、OB、AB切于E、F、P．

（1）在上述变化过程中：Rt△AOB的周长，⊙K的半径，△AOB外接圆半径，这几个量中不会发生变化的是什么？并简要说明理由；

（2）当AE = 4时，求⊙K的半径r；

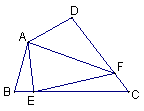
.已知，如图，在四边形ABCD中，∠B +∠D =180°，AB=AD，E、F分别是线段BC、CD上的点，且B E + FD= EF。

求证：∠EAF =∠BAD

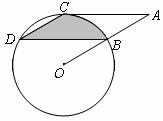
如图，点B、C、D都在⊙O上，过点C作AC∥BD交OB延长线于点A，连接CD，且∠CDB=∠OBD=30°，DB=6cm．

（1）求证：AC是⊙O的切线；

（2）求⊙O的半径长；

（3）求由弦CD、BD与弧BC所围成的阴影部分的面积（结果保留）．  

 已知：二次函数的表达式为．

（1）写出这个函数图象的对称轴和顶点坐标；并画出图像。

（2）求图象与轴的交点坐标；

（3）观察图象，指出使函数值y＞时自变量x的取值范围

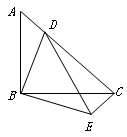
如图，等腰直角△ABC中，∠ABC=90°，点D在AC上，将△ABD绕顶点B沿顺时针方向旋转90°后得到△CBE.

⑴求∠DCE的度数；

⑵当AB=4，AD∶DC=1∶3时，求DE的长.