
科目: 来源: 题型:
中国旅游研究院最近发布报告称,2012年中国出境旅游人数8200万人次,8200万用科学计数法表示为( )
A.82×106 B.8.2×106 C.8.2×107 D. 8.2×108
查看答案和解析>>
科目: 来源: 题型:
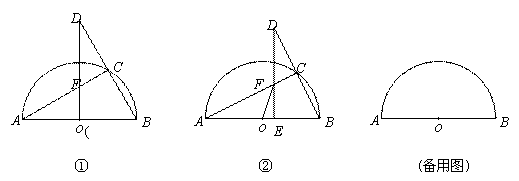
以AB为直径作半圆O,AB=10,点![]() C是该半圆上一动点,联结AC、BC,并延长BC至点D,使DC=BC,过点D作DE⊥AB于点E、交AC于点F,联结OF.
C是该半圆上一动点,联结AC、BC,并延长BC至点D,使DC=BC,过点D作DE⊥AB于点E、交AC于点F,联结OF.
(1)如图①,当点E与点O重合时,求∠BAC的度数;
(2)如图②,当DE=8时,求线段EF的长;
(3)在点C运动过程中,若点E始终在线段AB上,是否存在以点E、O、F为顶点的三角形与△ABC相似,若存在,请直接写出此时线段OE的长;若不存在,请说明理由.
 |
查看答案和解析>>
科目: 来源: 题型:
已知抛物线![]() 上有不同的两点E
上有不同的两点E![]() 和F
和F![]() .
.
(1)求此抛物线的解析式.
(2)如图,抛物线![]() 与x轴的正半轴和y轴分别交于点A和点B,M为AB的中点,∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.∠PMQ在AB的左侧以M为中心旋转,设AD 的长为m(m>0),BC的长为n,求n和m之间的函数关系式.
与x轴的正半轴和y轴分别交于点A和点B,M为AB的中点,∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.∠PMQ在AB的左侧以M为中心旋转,设AD 的长为m(m>0),BC的长为n,求n和m之间的函数关系式.
(3)在(2)的条件下,当m,n为何值时,∠PMQ的边过点F.
 |
查看答案和解析>>
科目: 来源: 题型:
如图①,P为△ABC内一点,联结PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称P为△ABC的自相似点.
(1)如图②,已知Rt△ABC中,∠ACB=90°,∠![]() ABC>∠A,CD是AB上的中线,过点B作BE⊥CD,垂足为E,请证明E是△ABC的自相似点.
ABC>∠A,CD是AB上的中线,过点B作BE⊥CD,垂足为E,请证明E是△ABC的自相似点.
(2)如图③,在△ABC中,∠A<∠B<∠C.若△ABC的内心P是该三角形的自相似点,
则∠A:∠B:∠C= .

查看答案和解析>>
科目: 来源: 题型:
小明爸爸经营的水果店出售一种优质热带水果,正在上初三的小明经过调查和计算,发现这种水果每月的销售量y(千克)![]() 与销售单价x(元)之间存在着一次函数关系:y=-10x+500.
与销售单价x(元)之间存在着一次函数关系:y=-10x+500.
下面是他们的一次对话:
小明:“您要是告诉我咱家这种水果的进价是多少?我就能帮你预测好多信息呢!”
爸爸:“咱家这种水果的进价是每千克20元”
聪明的你,也来解答一下小明想要解决的三个问题:
(1)若每月获得利润w(元)是销售单价x(元)的函数,求这个函数的解析式.
(2)当销售单价为多少元时,每月可获得最大利润?
(3)如果想要每月从这种水果的销售中获利2000元,那么销售单价应该定为多少元?
查看答案和解析>>
科目: 来源: 题型:
如图,△ABC内接于⊙O,AB=AC,过点A作AD⊥AB交⊙O于点D,交BC于点E,点F在DA的延长线上,且∠ABF=∠C .
(1)求证:BF是⊙O的切线;
(2)若AD=4,cos∠ABF=![]() ,求BC的长.
,求BC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com