
科目: 来源: 题型:
已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,以O 为原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标和过O、C、A三点的抛物线的解析式;
(2)P是此抛物线的对称轴上一动点,当以P、O、C为顶点的三角形是等腰三角形时,请直接写出点P的坐标;
(3)M(x,y)是此抛物线上一个动点,当△MOB的面积等于△OAB面积时,求M的坐标.

查看答案和解析>>
科目: 来源: 题型:
某企业为打入国际市场,决定从A、B两种产品中只选择一种进行投资生产.已知投资生产这两种产品的有关数据如下表:(单位:万美元)
| 项 目 类 别 | 年固定 成本 | 每件产品 成本 | 每件产品 销售价 | 每年最多可 生产的件数 |
| A产品 | 20 | m | 10 | 200 |
| B产品 | 40 | 8 | 18 | 120 |
其中年固定成本与年生产的件数无关,m为待定常数,其值由生产A产品的原材料价格决定,预计6≤m≤8.另外,年销售x件B产品时需上交0.05x2万美元的特别关税.假设生产出来的产品都能在当年销售出去.
(1)写出该厂分别投资生产A、B两种产品的年利润y1,y2与生产相应产品的件数x之间的函数关系并指明其自变量取值范围;
(2)如何投资才可获得最大年利润?请你做出规划.
查看答案和解析>>
科目: 来源: 题型:
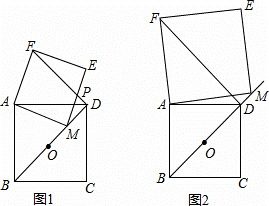
已知点O为正方形ABCD的中心,M为射线OD上一动点(M与点O,D不重合),以线段AM为一边作正方形AMEF,连接FD.
(1)当点M在线段OD上时(如图1),线段BM与DF有怎样的数量及位置关系?请判断并直接写出结果;
(2)当点M在线段OD的延长线上时(如图2),(1)中的结论是否仍然成立?请结合图2说明理由.
查看答案和解析>>
科目: 来源: 题型:
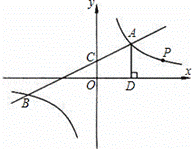
如图,一次函数y1=k1x+2与反比例函数![]() 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
(1)k1= _________ ,k2= _________ ;
(2)根据函数图象可知,当y1>y2时,x的取值范围是 _________ ;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
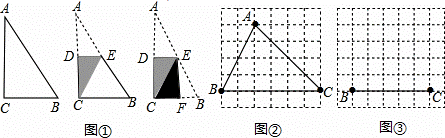
如图①,将一张直角三角形纸片△ABC折叠,使点A与点C重合,这时DE为折痕,△CBE为等腰三角形;再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.
(1)如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕;
(2)如图③,在正方形网格中,以给定的BC为一边,画出一个斜三角形ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形;
(3)若一个三角形所折成的“叠加矩形”为正方形,那么它必须满足的条件是什么?
查看答案和解析>>
科目: 来源: 题型:阅读理解
先阅读,再利用其结论解决问题.
阅读:已知一元二次方程ax2+bx+c=0(a≠0)的两个实根为x1,x2,则有x1+x2=﹣,x1•x2=.这个结论是法国数学家韦达最先发现并证明的,故把它称为“韦达定理”.利用此定理,可以不解方程就得出x1+x2和 x1•x2的值,进而求出相关的代数式的值.
解决问题:对于一切不小于2的自然数n,关于x的一元二次方程x2﹣(n+2)x﹣2n2=0的两个根记作an,bn(n≥2),
请求出
![]()
![]() +…
+…![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
在学校组织的科学常识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
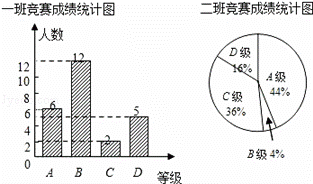
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分以上(包括70分)的人数为 _________ ;
(2)请你将表格补充完整:
| 平均数(分) | 中位数(分) | 众数(分) | |
| 一班 | 77.6 | 80 | |
| 二班 | 90 |
(3)请从不同角度对这次竞赛成绩的结果进行分析.(至少两个角度)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com