
科目: 来源: 题型:
如图,已知抛物线y=a(x-1)2+![]() (a≠0)经过点A(-2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点D平行于
(a≠0)经过点A(-2,0),抛物线的顶点为D,过O作射线OM∥AD.过顶点D平行于![]() 轴的直线交射线OM于点C,B在
轴的直线交射线OM于点C,B在![]() 轴正半轴上,连结BC.
轴正半轴上,连结BC.
(1)求该抛物线的解析式;
(2)①若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为t(s).问:当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?
②若OC=OB,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t(s),连接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.

查看答案和解析>>
科目: 来源: 题型:
某超市计划上两个新项目:
项目一:销售A种商品,所获得利润y(万元)与投资金额![]() (万元)之间存在正比例函数关系:
(万元)之间存在正比例函数关系:![]() .当投资5万元时,可获得利润2万元;
.当投资5万元时,可获得利润2万元;
项目二:销售B种商品,所获得利润y(万元)与投资金额![]() (万元)之间存在二次函数关系:
(万元)之间存在二次函数关系:![]() .当投资4万元时,可获得利润3.2万元;当投资2万元时,可获得利润2.4万元.
.当投资4万元时,可获得利润3.2万元;当投资2万元时,可获得利润2.4万元.
⑴ 请分别求出上述的正比例函数表达式和二次函数表达式;
⑵ 如果超市同时对A、B两种商品共投资12万元,请你设计一个能获得最大利润的投资方案,并求出按此方案获得的最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=4,点P是斜边AB上一个动点,点D是CP的中点,延长BD至E,使DE=BD,连结AE.
⑴ 求四边形PCEA的面积;
⑵ 当AP的长为何值时,四边形PCEA是平行四边形;
⑶ 当AP的长为何值时,四边形PCEA是直角梯形.

查看答案和解析>>
科目: 来源: 题型:
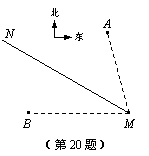
如图,气象部门预报:在海面上生成了一股较强台风,在距台风中心60千米的圆形区域内将会受严重破坏.台风中心正从海岸M点登陆,并以72千米/时的速度沿北偏西60°的方向移动.已知M点位于A城的南偏东15°方向,距A城![]() 千米;M点位于B城的正东方向,距B城
千米;M点位于B城的正东方向,距B城![]() 千米.
千米.
假设台风在移动过程中,其风力和方向保持不变,请回答下列问题:
⑴ A城和B城是否会受到此次台风的侵袭?并说明理由;
⑵ 若受到此次台风侵袭,该城受到台风侵袭的持续时间有多少小时?
 |
查看答案和解析>>
科目: 来源: 题型:
某高级中学要印制宣传册,联系了甲、乙两家印刷厂.甲厂的优惠条件是:按每份定价1.5元的8折收费,另收900元的制版费;乙厂的优惠条件是:每份定价1.5元的价格不变,而制版费900元则按4折优惠,且甲、乙两厂都规定:一次印刷数量不低于1000份.
⑴ 分别求出两家印刷厂收费![]() (元)与印刷数量
(元)与印刷数量![]() (份)的函数关系式,并指出自变量
(份)的函数关系式,并指出自变量![]() 的取值范围;
的取值范围;
⑵ 如何根据印刷数量选择比较合算的方案?如果该中学要印制3000份宣传册,那么应当选择哪家印刷厂?需要多少费用?
查看答案和解析>>
科目: 来源: 题型:
某超市有A、B、C三种型号的甲种品牌饮水机和D、E两种型号的乙种品牌饮水机,某中学准备从甲、乙两种品牌的饮水机中各选购一种型号的饮水机安装到教室.
⑴ 写出所有的选购方案,如果各种选购方案被选中的可能性相同,那么A型号饮水机被选中的概率是多少?
⑵ 如果该学校计划用1万元人民币购买甲、乙两种品牌的饮水机共24台(价格如表格所示),其中甲种品牌饮水机选为A型号的,请你算算该中学购买到A型号饮水机共多少台?
| 品 牌 | 甲 | 乙 | |||
| 型 号 | A | B | C | D | E |
| 单价(元) | 600 | 400 | 250 | 500 | 200 |
查看答案和解析>>
科目: 来源: 题型:
如图,等腰梯形ABCD中,AD∥BC,延长BC到E,使CE=AD.
⑴ 用尺规作图法,过点D作DM⊥BE,垂足为M(不写作法,保留作图痕迹);
 ⑵判断BM、ME的大小关系,并说明理由.
⑵判断BM、ME的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com