
科目: 来源: 题型:
如图①,已知点D在AB上,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,且M为EC的中点.
(1)连接DM并延长交BC于N,求证:CN=AD;
(2)求证:△BMD为等腰直角三角形;
(3)将△ADE绕点A逆时针旋转90°时(如图②所示位置),△BMD为等腰直角三角形的结论是否仍成立?若成立,请证明:若不成立,请说明理由.
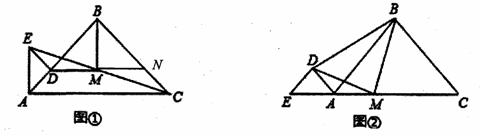
查看答案和解析>>
科目: 来源: 题型:
已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF//AB,BF的延长线交DC于点E.
(1)求证:△BFC≌△DFC;
(2)求证:AD=DE;
(3)若△DEF的周长为6,AD=2,BC=5,求梯形ABCD的面积.

查看答案和解析>>
科目: 来源: 题型:
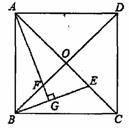
如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
(1)试说明OE=OF;
(2)当AE=AB时,过点E作EH⊥BE交AD边于H.若
该正方形的边长为1,求AH的长.
 |
查看答案和解析>>
科目: 来源: 题型:
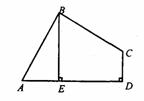
已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
 |
查看答案和解析>>
科目: 来源: 题型:
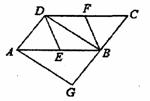
如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证四边形DEBF是菱形.
查看答案和解析>>
科目: 来源: 题型:
如图,在直角梯形ABCD中,AD∥BC,DC⊥BC,
∠B=60°,BC=2AD,E、F分别为AB、BC的中点.
求证:(1)四边形AFCD为矩形;
(2)FE⊥DE.

查看答案和解析>>
科目: 来源: 题型:
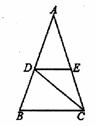
如图,等腰三角形ABC的顶角∠A=36°,CD
是底角∠ACB的平分线,DE∥BC.
(1)求证:△CDE是等腰三角形;
(2)图中除了△ABC和△CDE外还有等腰三角形,请直接写出这
些等腰三角形.
 |
查看答案和解析>>
科目: 来源: 题型:
如图,网格中的图案是美国总统Garfie1d于1876年给出的一种验证某个著名结论的方法:
(1)请你画出直角梯形EDBC绕EC中点O顺时针方向旋转180°
的图案,你会得到一个美丽的图案.(阴影部分不要涂错).
(2)若网格中每个小正方形边长为单位1,旋转后A、B、D的对应
点为A'、B'、D',求四边形ACA'E的面积?
(3)根据旋转前后形成的这个美丽图案,你能说出这个著名的结论
吗?若能,请你写出这个结论.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com