某学校用420元钱到商场去购买“84”消毒液，经过还价，每瓶便宜0.5元，结果比用原价多买了20瓶，求原价每瓶多少元？若设原价每瓶元，则可列出方程为         （     ）

A．          B．

C．          D．

函数中自变量的取值范围是（       ）

     A、      B、       C、       D、

根据下图所示程序计算函数值，若输入的的值为，则输出的函数值为（    ）

A．　　　　              

B．    

C．　  　　             

D．

设a,b,c分别是△ABC的三条边，且∠A=60º,那么的值是（      ）

A.1               B.0.5            C.2                    D.3

李明为好友制作一个（如图）正方体礼品盒，六面上各有一字，连起来就是“预祝中考成功”，其中“预”的对面是“中”，“成”的对面是“功”，则它的平面展开图可能是（      ）

已知（     ）   

A.6              B.9              C.12                   D.81 

2005年5月22日中华人民共和国登山队成功登上珠穆朗玛峰峰顶，再次精确测量珠峰高度，珠峰新高度为8844.43米（从右图看出峰顶位于中国境内），它的高度更接近于（     ） 

A．    B．    C．          D．

 如图，平面直角坐标系中，点A（0，4），B（3，0），D、E在x轴上，F为平面上一点，且EF⊥x轴，直线DF与直线AB互相垂直，垂足为H，△AOB≌△DEF，设BD＝h。

（1）若F坐标（7，3），则h＝          ，若F坐标（－10，－3），则DH＝       ；

（2）如h＝，则相对应的F点存在      个，并请求出恰好在抛物线y＝ 上的点F的坐标；

（3）请求出4个h值，满足以A、H、F、E为顶点的四边形是梯形。

平面直角坐标中，直线OA、OB都经过第一象限（O是坐标原点），且满足

∠AOB＝45°，如直线OA的解析式为y＝kx，现探究直线OB解析式情况。

（1）       当∠BOX＝30°时（如图1），求直线OB解析式；

（2）       当k＝2时（如图2），探究过程：OA上取一点P（1, 2）

作PF⊥x轴于F，交OB于E，作EH⊥OA于H，

则＝        ，根据以上探究过程，请求出直线

OB解析式；

（3）       设直线OB解析式为y＝mx，则

m＝                      （用k表示），如

   双曲线交OA于M， 交OB于N，当OM＝ON时，

求k的值。

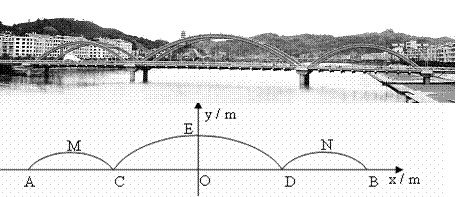
许多桥梁都采用抛物线型设计，小明将他家乡的彩虹桥按比例缩小后，绘成如下的示意图，图中的三条抛物线分别表示桥上的三条钢梁，x轴表示桥面，y轴经过中间抛物线的最高点，左右两条抛物线关于y轴对称。经过测算，中间抛物线的解析式为

y＝－x²＋10，并且BD＝CD。

（1）求钢梁最高点离桥面的高度OE的长；

（2）求桥上三条钢梁的总跨度AB的长；

（3）若拉杆DE∥拉杆BN，求右侧抛物线的解析式。