
科目: 来源: 题型:
答案:(1)如图
(2)答:这条船继续前进,没有被浅滩阻碍的危险。
解:作CD⊥直线AB于点D,
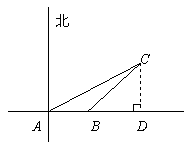 由已知可得∠CAD=30°, ∠CBD=45°,
由已知可得∠CAD=30°, ∠CBD=45°,
AB=100米。
设CD=![]() 米。
米。
在Rt△ACD中
tan∠CAD=![]()
∴AD=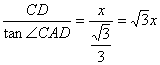
在Rt△CBD中
∵∠CBD=45°, ∴BD=CD=x,
∵AD-BD=AB, ∴![]() 。
。
解得![]()
∴这条船继续前进没有被浅滩阻碍的危险。
查看答案和解析>>
科目: 来源: 题型:
【解】当α=70°时,梯子顶端达到的最大高度,
∵sinα=![]() ,
,
∴AC = sin70°×6≈0.94×6=5.64≈5.6(米)
答:人安全攀爬梯子时,梯子的顶端达到的最大高度约5.6米.
查看答案和解析>>
科目: 来源: 题型:
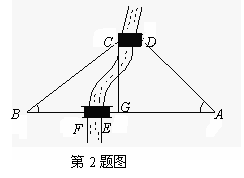
如图所示,A、B两地之间有一条河,原来从A地到B 地需要经过DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.已知BC=10km,∠A=45°,∠B=37°,桥DC和AB平行.
(1)求两桥之间的距离CG(CGAB);
(2)从A地到达B地可比原来少走多少路程?
(精确到0.1 km).(参考数据:![]() sin37°≈0.60,cos37°≈0.80
sin37°≈0.60,cos37°≈0.80
 |
答案:(1)CG=6km;
(2)作DH⊥AB,得到DH=HA=6,AD=![]() ,
,
所以少走的路程是(AD+CD+BC)-(BG+GH+AH)=![]() +10-14≈4.5km.
+10-14≈4.5km.
查看答案和解析>>
科目: 来源: 题型:
日本福岛出现核电站事故后,我国国家海洋局高度关注事态发展,紧急调集海上巡逻的海检船,在相关海域进行现场监测与海水采样,针对核泄漏在极端情况下对海洋环境的影响及时开展分析评估.如图2-6,上午9时,海检船位于A处,观测到某港口城市P位于海检船的北偏西67.5°方向,海检船以21海里/时的速度向正北方向行驶,下午2时海检船到达B处,这时观察到城市P位于海检船的南偏西36.9°方向,求此时海检船所在B处与城市P的距离?
![]()
![]()
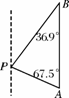
图2-6
查看答案和解析>>
科目: 来源: 题型:
某市为缓解城市交通压力,决定修建人行天桥,原设计天桥的楼梯长AB=6 m,
∠ABC=45°,后考虑到安全因素,将楼梯脚B移到CB延长线上点D处,使∠ADC=30°(如图1-4所示).
(1)求调整后楼梯AD的长;
(2)求BD的长(结果保留根号).
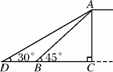
图1-4
查看答案和解析>>
科目: 来源: 题型:
 2011年3月11日13时46分日本发生了9.0级大地震,伴随着就是海啸。山坡上有一棵与水平面垂直的大树, 海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m。
2011年3月11日13时46分日本发生了9.0级大地震,伴随着就是海啸。山坡上有一棵与水平面垂直的大树, 海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m。
(1)求∠DAC的度数;
(2)求这棵大树折断前AB的高?(结果精确到个位,参考数据:![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
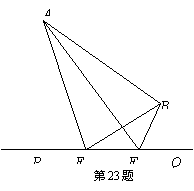
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
(1)判断AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).(参考数据:![]() ≈1.73,
≈1.73,
 sin74°≈0.96,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)
sin74°≈0.96,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com