—3的倒数为（      ）

A、3            B、—             C、               D、–3

如图，某同学在大楼30m高的窗口看地面上两辆汽车B、C，测得俯角分别为60°和45°，如果汽车B、C在与该楼的垂直线上行使，求汽车C与汽车B之间的距离．（精确到0.1m，参考数据：，）

已知：如图6，在△ABC中， CD⊥AB，sinA=，AB=13，CD=12，

求AD的长和tanB的值.

．

解：作BE⊥l于点E，DF⊥l于点F．                   ……2分

∵∠α+∠DAF=180°-∠BAD=180°-90°=90°，∠ADF+∠DAF=90°，

∴∠ADF=∠α=36°．根据题意，得BE=24mm, DF=48mm． ……4分

在Rt△ABE中，sinα=BE/AB，∴AB=BE/sin36°=40(mm).……6分

在Rt△ADF中，cos∠ADF=DF/AD，∴AD=DF/COS36°=60(mm）．8分

∴矩形ABCD的周长=2(40+60)=200(mm)．             ……10分

解：如图所示，过点A、D分别作BC的垂线AE、DF分别交BC于点E、F，------1分

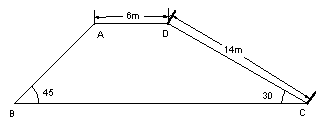所以△ABE、△CDF均为Rt△，

又因为CD＝14，∠DCF＝30°，

所以DF＝7＝AE，-----------------------4分

所以FC＝7_≈12.1 ------------------6分

所以BC＝7＋6＋12.1＝25.1m．------8分

答案：解：过D作DM⊥AE于M，过C作CN⊥AE于N，则：MN=CD=3米，设AM=x，则AN=x+3， 由题意：∠ADM =30^ｏ，∠ACN =45^ｏ，

在Rt△ADM中，DM=AM·cot30^ｏ=x，在Rt△ANC中，CN=AN=x+3，

又DM=CN=MB，∴x=x+3，解之得，x=（+1），∴AB=AM+MB=x+x+3=2×（+1）+3=3+6≈11（米）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 y=1

如图，为测量某塔AB的高度，在离塔底部10米处目测其塔顶A，仰角为60°，目高1.5米，试求该塔的高度。（≈1.41，≈1.73）

如图，某校一幢教学大楼的顶部竖有一块“传承文明，启智求真”的宣传牌CD．小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°，沿山坡向上走到B处测得宣传牌顶部C的仰角为45°．已知山坡AB的坡度i＝1:，AB＝10米，AE＝15米，求这块宣传牌CD的高度．（测角器的高度忽略不计，结果精确到0.1米．参考数据：≈1.414，≈1.732）(7分)

解：（1）△AFB∽△FEC. 

证明：由题意得：∠AFE=∠D=90° 又∠B=∠C=90°

 ∴∠BAF+∠AFB=90° , ∠EFC+∠AFB=90°

∴∠BAF=∠EFC     ∴    AFB∽△FEC

（2）设EC=3x,FC=4x，则有DE=EF=5x ，∴AB=CD=3x+ 5x=8x

由△AFB∽△FEC得：     即： =  ∴BF=6x   ∴BC=BF－CF=6x+ 4x= 10x

∴在Rt△ADE中，AD=BC=10x，AE=，则有

解得（舍去）   ∴AB+BC+CD+DA=36x=36(cm)    答：矩形ABCD的周长为36cm.