
科目: 来源: 题型:
下列各式由左到右的变形中,是因式分解的为( )
A、a(x+y)=ax+ay; B、x2-4x+4=x(x-4)+4;
C、10x2-5x=5x(2x-1); ![]() D、x2-16+3x=(x+4)(x-4)+3x
D、x2-16+3x=(x+4)(x-4)+3x
查看答案和解析>>
科目: 来源: 题型:
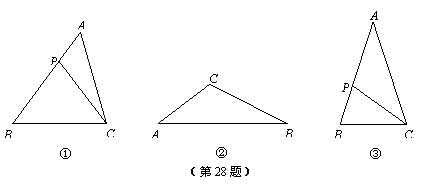
(1)如图①,P为△ABC的边AB上一点(P不与点A、点B重合),连接PC,如果△CBP∽△ABC,那么就称P为△ABC的边AB上的相似点.
画法初探
①如图②,在△ABC中,∠ACB>90°,画出△ABC的边AB上的相似点P(画图工具不限,保留画图痕迹或有必要的说明);
 |
辩证思考
②是不是所有的三角形都存在它的边上的相似点?如果是,请说明理由;如果不是,请找出一个不存在边上相似点的三角形;
特例分析
③已知P为△ABC的边AB上的相似点,连接PC,若△ACP∽△ABC,则△ABC的形状是 ▲ ;
④如图③,在△ABC中,AB=AC,∠A=36°,P是边AB上的相似点,求![]() 的值.
的值.
(2)在矩形ABCD中,AB=a,BC=b(a≥b).P是AB上的点(P不与点A、点B重合),作PQ⊥CD,垂足为Q.如果矩形ADQP∽矩形ABCD,那么就称PQ为矩形ABCD的边AB、CD上的相似线.
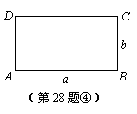 ①类比(1)中的“画法初探”,可以提出问题:对于如图④的矩形ABCD,在不限制画图工具的前提下,如何画出它的边AB、CD上的相似线PQ呢?
①类比(1)中的“画法初探”,可以提出问题:对于如图④的矩形ABCD,在不限制画图工具的前提下,如何画出它的边AB、CD上的相似线PQ呢?
你的解答是: ▲ (只需描述PQ的画法,不需在图上画出PQ).
②请继续类比(1)中的“辩证思考”、“特例分析”两个栏目对矩形的相似线进行研究,要求每个栏目提出一个问题并解决.
查看答案和解析>>
科目: 来源: 题型:
某汽车销售公司10月份销售某厂家的汽车.在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出1部汽车,则该部汽车的进价为30万元;每多售出1部,所有售出的汽车的进价均降低0.2万元/部.
(1)若该公司当月售出2部汽车,则每部汽车的进价为 ▲ 万元;
(2)如果汽车的售价为31万元/部.
①写出公司当月盈利y(万元)与汽车销售量x(部)之间的函数关系式;
②若该公司当月盈利28万元,求售出汽车的数量.
查看答案和解析>>
科目: 来源: 题型:
问题:已知线段AB、CD相交于点O,AB=CD.连接AD、BC,请添加一个条件,使得△AOD≌△COB.
 小明的做法及思路
小明的做法及思路
小明添加了条件:∠DAB=∠BCD.他的思路是:
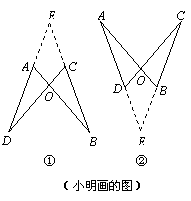 分两种情况画图①、图②,在两幅图中,
分两种情况画图①、图②,在两幅图中,
都作直线DA、BC,两直线交于点E.
由∠DAB=∠BCD,可得∠EAB=∠ECD.
∵AB=CD,∠E=∠E,
∴△EAB≌△ECD.∴EB=ED,EA=EC.
图①中ED-EA=EB-EC,即AD=CB.
图②中EA-ED=EC-EB,即AD=CB.
又∵∠DAB=∠BCD,∠AOD=∠COB,
∴△AOD≌△COB.
数学老师的观点
(1)数学老师说:小明添加的条件是错误的,请你给出解释.
你的想法
(2)请你重新添加一个满足问题要求的条件,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
如图,在△ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D.
(1)作⊙O,使⊙O经过A、C、D三点(尺规作图,保留作图痕迹,不写作法);
(2)判断直线 BC与⊙O的位置关系,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
小轿车从甲地出发驶往乙地,同时货车从相距乙地60 km的入口处驶往甲地(两车均在甲、乙两地之间的公路上匀速行驶),下图是它们离甲地的路程y(km)与货车行驶时间x(h)之间的函数的部分图象.
(1)求货车离甲地的路程y(km)与它的行驶时间x(h)的函数关系式;
(2)哪一辆车先到达目的地?说明理由.

查看答案和解析>>
科目: 来源: 题型:
某校九年级男生进行引体向上训练,体育老师随机选择了部分男生,根据训练前成绩编组:0~4个的编为第一组,5~8个的编为第二组,9~12个的编为第三组,在训练后制作了如下两幅统计图,请回答下列问题:
 |
(1)下列说法正确的是 ▲ (填写所有正确的序号).
①训练后,第一组引体向上平均成绩的增长率最大;
②训练前,所选男生引体向上成绩的中位数一定在第二组;
③训练前,所选男生引体向上成绩的众数一定在第二组.
(2)估计该校九年级全体男生训练后的平均成绩是多少?
查看答案和解析>>
科目: 来源: 题型:
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC平面上的一动点,连接OB、OC,G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)如图,当点O在△ABC内时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,点O所在位置应满足什么条件?(直接写出答案,不需说明理由.)

查看答案和解析>>
科目: 来源: 题型:
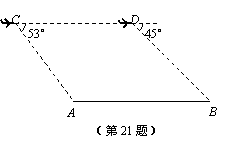
飞机测量一岛屿两端A、B的距离,在距海平面垂直高度为200 m的点C处测得A的俯角为53°,然后沿着平行于AB的方向水平飞行了300 m,在点D处测得B的俯角为45°,求岛屿两端A、B的距离.(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
 |
查看答案和解析>>
科目: 来源: 题型:
从甲地到乙地有A1、A2两条路线,从乙地到丙地有B1、B2、B3三条路线,其中A1B2是从甲地到丙地的最短路线.一个人任意选了一条从甲地到丙地的路线,他恰好选到最短路线的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com