下列运算正确的是（    ）

在平面直角坐标系中，点在第（    ）象限．

  一               二                  三                四

已知一个多边形的内角和是，则这个多边形是（      ）

  四边形             五边形            六边形           七边形

如下左图是由6个大小相同的正方体组成的几何体，它的左视图是（     ）

 气候宜人的省级度假旅游胜地吴川吉兆，测得一至五月份的平均气温分别为17、17、20、22、24（单位：），这组数据的中位数是（    ）

  国家提倡“低碳减排”，湛江某公司计划在海边建风能发电站，电站年均发电量约为度，若将数据用科学记数法表示为（    ）

 下列各数中，最小的数是（    ）

 1                                                 

已知抛物线抛物线y _n=-(x-a_n)²+a_n（n为正整数，且0<a₁<a₂<…<a_n）与x轴的交点为A_n-1（b_n-1,0）和A_n(b_n，0)，当n=1时，第1条抛物线y₁=-(x-a₁)²+a₁与x轴的交点为A₀（0，0）和A₁（b₁，0），其他依此类推．

（1）求a₁,b₁的值及抛物线y₂的解析式；

（2）抛物线y₃的顶点坐标为（     ，     ）；

     依此类推第n条抛物线y_n的顶点坐标为（       ，      ）;

     所有抛物线的顶点坐标满足的函数关系是                  ；

（3）探究下列结论：

     ①若用A_n-1A_n表示第n条抛物线被x轴截得得线段长，直接写出A₀A₁的值，并求出A_n-1A_n；

②是否存在经过点A（2，0）的直线和所有抛物线都相交，且被每一条抛物线截得得线段的长度都相等？若存在，直接写出直线的表达式；若不存在，请说明理由．

某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：

　　●操作发现：

      在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME，则下列结论正确的是         （填序号即可）

     ①AF=AG=AB；②MD=ME；③整个图形是轴对称图形；④∠DAB=∠DMB．

●数学思考：

  在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图2所示，M是BC的中点，连接MD和ME，则MD和ME具有怎样的数量和位置关系？请给出证明过程；

●类比探索：

  在任意△ABC中，仍分别以AB和AC为斜边，向△ABC的内侧作等腰直角三角形，如图3所示，M是BC的中点，连接MD和ME，试判断△MED的形状．

  答：           ．

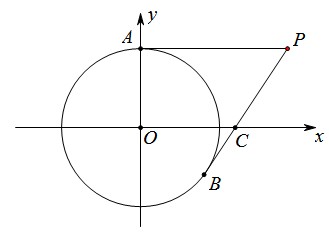
如图，在平面直角坐标系中，以点O为圆心，半径为2的圆与y轴交于点A，点P（4，2）是⊙O外一点，连接AP，直线PB与⊙O相切于点B，交x轴于点C．

（1）证明PA是⊙O的切线；

（2）求点B的坐标；

（3）求直线AB的解析式．