已知：如图，AB为⊙O的直径，AB⊥AC，BC交⊙O于D，E是AC的中点，ED与AB的延长线相交于点F．

（1）求证：DE为⊙O的切线．

（2）求证：AB：AC=BF：DF．

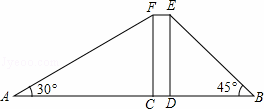
小明、小华在一栋电梯楼前感慨楼房真高．小明说：“这楼起码20层！”小华却不以为然：“20层？我看没有，数数就知道了！”小明说：“有本事，你不用数也能明白！”小华想了想说：“没问题！让我们来量一量吧！”小明、小华在楼体两侧各选A、B两点，测量数据如图，其中矩形CDEF表示楼体，AB=150米，CD=10米，∠A=30°，∠B=45°，（A、C、D、B四点在同一直线上）问：

（1）楼高多少米？

（2）若每层楼按3米计算，你支持小明还是小华的观点呢？请说明理由．（参考数据：≈1.73，≈1.41，≈2.24）

甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地，如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系；折线BCD表示轿车离甲地距离y（千米）与x（小时）之间的函数关系．请根据图象解答下列问题：

（1）轿车到达乙地后，货车距乙地多少千米？

（2）求线段CD对应的函数解析式．

（3）轿车到达乙地后，马上沿原路以CD段速度返回，求轿车从甲地出发后多长时间再与货车相遇（结果精确到0.01）．

一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“鄂”、“州”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球．

（1）若从中任取一个球，球上的汉字刚好是“鄂”的概率为多少？

（2）甲从中任取一球，不放回，再从中任取一球，请用树状图的方法，求出甲取出的两个球上的汉字恰能组成“灵秀”或“鄂州”的概率P₁；

（3）乙从中任取一球，记下汉字后再放回袋中，然后再从中任取一球，记乙取出的两个球上的汉字恰能组成“灵秀”或“鄂州”的概率为P₂，指出P₁，P₂的大小关系（请直接写出结论，不必证明）．

如图正方形ABCD的边长为4，E、F分别为DC、BC中点．

（1）求证：△ADE≌△ABF．

（2）求△AEF的面积．

先化简，后求值：，其中a=3．

如图，△AOB中，∠AOB=90°，AO=3，BO=6，△AOB绕顶点O逆时针旋转到△A′OB′处，此时线段A′B′与BO的交点E为BO的中点，则线段B′E的长度为　　．

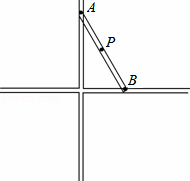
著名画家达芬奇不仅画艺超群，同时还是一个数学家、发明家．他曾经设计过一种圆规如图所示，有两个互相垂直的滑槽（滑槽宽度忽略不计），一根没有弹性的木棒的两端A、B能在滑槽内自由滑动，将笔插入位于木棒中点P处的小孔中，随着木棒的滑动就可以画出一个圆来．若AB=20cm，则画出的圆的半径为　10　cm．

已知正比例函数y=﹣4x与反比例函数的图象交于A、B两点，若点A的坐标为（x，4），则点B的坐标为　（1，﹣4）　．

若不等式组的解集为3≤x≤4，则不等式ax+b＜0的解集为　x＞　．