
科目: 来源: 题型:
如图,▱ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )

|
| A. | 36° | B. | 46° | C. | 27° | D. | 63° |
查看答案和解析>>
科目: 来源: 题型:
已知一元二次方程:①x2+2x+3=0,②x2﹣2x﹣3=0.下列说法正确的是( )
|
| A. | ①②都有实数解 | B. | ①无实数解,②有实数解 |
|
| C. | ①有实数解,②无实数解 | D. | ①②都无实数解 |
查看答案和解析>>
科目: 来源: 题型:
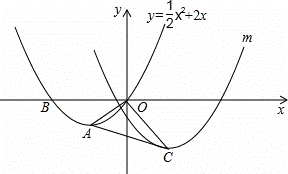
如图,在平面直角坐标系中,O为坐标原点,抛物线y=![]() x2+2x与x轴相交于O、B,顶点为A,连接OA.
x2+2x与x轴相交于O、B,顶点为A,连接OA.
(1)求点A的坐标和∠AOB的度数;
(2)若将抛物线y=![]() x2+2x向右平移4个单位,再向下平移2个单位,得到抛物线m,其顶点为点C.连接OC和AC,把△AOC沿OA翻折得到四边形ACOC′.试判断其形状,并说明理由;
x2+2x向右平移4个单位,再向下平移2个单位,得到抛物线m,其顶点为点C.连接OC和AC,把△AOC沿OA翻折得到四边形ACOC′.试判断其形状,并说明理由;
(3)在(2)的情况下,判断点C′是否在抛物线y=![]() x2+2x上,请说明理由;
x2+2x上,请说明理由;
(4)若点P为x轴上的一个动点,试探究在抛物线m上是否存在点Q,使以点O、P、C、Q为顶点的四边形是平行四边形,且OC为该四边形的一条边?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=![]() .
.
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.

查看答案和解析>>
科目: 来源: 题型:
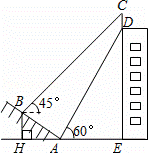
如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目: 来源: 题型:
如图,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于A(﹣2,m),B(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D.
的图象交于A(﹣2,m),B(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D.
(1)求这两个函数的解析式:
(2)求△ADC的面积.

查看答案和解析>>
科目: 来源: 题型:
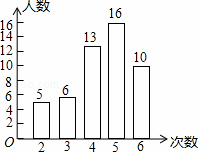
(1)我市开展了“寻找雷锋足迹”的活动,某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题:
①所调查的七年级50名学生在这个月内做好事次数的平均数是 4.4 ,众数是 5 ,极差是 6 :
②根据样本数据,估计该校七年级800名学生在“学雷锋活动月”中做好事不少于4次的人数.
(2)甲口袋有2个相同的小球,它们分别写有数字1和2;乙口袋中装有3个相同的小球,它们分别写有数字3、4和5,从这两个口袋中各随机地取出1个小球.
①用“树状图法”或“列表法”表示所有可能出现的结果;
②取出的两个小球上所写数字之和是偶数的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com