
科目: 来源: 题型:
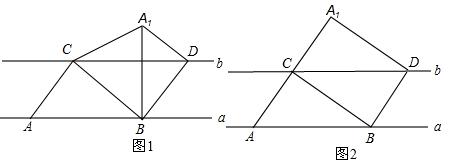
如图,A、B是直线![]() 上的两个定点,点C、D在直线
上的两个定点,点C、D在直线![]() 上运动(点C在点D的左侧),AB=CD=6cm,已知
上运动(点C在点D的左侧),AB=CD=6cm,已知![]() //
//![]() ,连接AC、BD、BC,把
,连接AC、BD、BC,把![]() 沿BC折叠得
沿BC折叠得![]() .
.
问题1:当![]() 、D两点重合时,则AC=___________cm;
、D两点重合时,则AC=___________cm;
问题2:当![]() 、D两点不重合时,连接
、D两点不重合时,连接![]() ,可探究发现
,可探究发现![]() ,
,
下面是小明的思考:
(1)将![]() 沿BC翻折,点A关于直线BC的对称点为
沿BC翻折,点A关于直线BC的对称点为![]() ,连接
,连接![]() 交BC所在直线于点M,由轴对称的性质,得
交BC所在直线于点M,由轴对称的性质,得![]() ,这一关系在变化过程中保持不变.
,这一关系在变化过程中保持不变.
(2)因为四边形ABCD是平行四边,设对角线的交点是O,易知![]() ,这一关系在变化过程中也保持不变。
,这一关系在变化过程中也保持不变。
请你借助于小明的思考,说明![]() 的理由。
的理由。
问题3:当![]() 、D两点不重合时,若直线
、D两点不重合时,若直线![]() 间的距离为
间的距离为![]() cm,且以点
cm,且以点![]() 为顶点的四边形是矩形,求AC的长。
为顶点的四边形是矩形,求AC的长。
查看答案和解析>>
科目: 来源: 题型:
(1)用配方法解一元二次方程![]() ,配方的过程可以用拼图直观表示.
,配方的过程可以用拼图直观表示.
把方程![]() 变形为
变形为![]() ,即
,即![]() 。
。
配方的过程,可以看成将一个长为![]() 、宽为
、宽为![]() 、面积为24的矩形割补成一个正方形,请在图①中“?” 处补全“拼成一个正方形”过程的图;
、面积为24的矩形割补成一个正方形,请在图①中“?” 处补全“拼成一个正方形”过程的图;
(2)现有长为![]() ,宽为
,宽为![]() 、面积为
、面积为![]() 的矩形
的矩形![]() ,b、c为常数,如图,你能利用四个这样相同的矩形构造1个图形,并利用你的拼图直观描述方程
,b、c为常数,如图,你能利用四个这样相同的矩形构造1个图形,并利用你的拼图直观描述方程![]() 的求解过程吗?请在图②的位置画图并说明.
的求解过程吗?请在图②的位置画图并说明.
 | |||
| |||
![]()
 | |||||||||||
 | |||||||||||
| |||||||||||
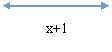 | |||||||||||

查看答案和解析>>
科目: 来源: 题型:
如图,在![]() 中,AB=AC,射线
中,AB=AC,射线![]() ,点P从点A出发沿射线AM运动,同时点Q从点B出发沿射线BC运动,设运动时间为
,点P从点A出发沿射线AM运动,同时点Q从点B出发沿射线BC运动,设运动时间为![]() .
.
(1)连接PQ、AQ、PC,当PQ经过AC的中点D时,求证:四边形AQCP是平行四边形;
(2)若BC=6cm,点P速度为1cm/s,点Q的速度为4cm/s,填空:
①当t为_____________s时,以A、Q、C、P为顶点的四边形是平行四边形;
②当t为_____________s时,以A、Q、C、P为顶点的四边形是直角梯形;

查看答案和解析>>
科目: 来源: 题型:
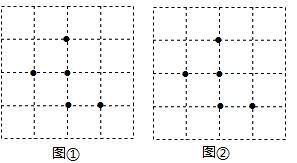
图①、图②都是![]() 的正方形网格,每个正方形的顶点称为格点,每个正方形的边长为1,在每个网格中标注了5个格点.按下列要求画图:
的正方形网格,每个正方形的顶点称为格点,每个正方形的边长为1,在每个网格中标注了5个格点.按下列要求画图:
(1)在图①中以格点为顶点画一个等腰三角形,使其内部已标注的格点只有3个;
(2)在图②中,以格点为顶点,画一个正方形,使其内部已标注的格点只有3个,且边长为无理数.
查看答案和解析>>
科目: 来源: 题型:
知识回顾
在学习《二次根式》时,我们知道:![]()
在学习《勾股定理》时,由于![]() 、
、![]() 、
、![]() 满足等式
满足等式![]() ,因此以
,因此以![]() 、
、![]() 、
、![]() 为边长的线段能构成直角三角形.
为边长的线段能构成直角三角形.
探索思考
请通过构造图形来说明:![]() .(画出图形并进行必要的解释)
.(画出图形并进行必要的解释)

查看答案和解析>>
科目: 来源: 题型:
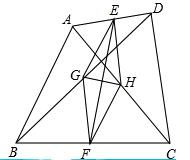
如图,在四边形ABCD中,AB=CD,E、F分别是AD、BC的中点,G、H分别是对角线BD、AC的中点.
(1)求证:四边形EGFH是菱形;
(2)若AB=1,则当![]() 时,求四边形EGFH的面积.
时,求四边形EGFH的面积.
查看答案和解析>>
科目: 来源: 题型:
甲、乙两人参加射击选拔赛,各射击了5次,成绩如下表(单位:环):
甲、乙两人射击成绩统计表
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 甲 | 9 | 4 | 7 | 4 | 6 |
| 乙 | 7 | 5 | 7 | 4 | 7 |
小明计算了甲射击成绩的平均数和方差:
| 解: |
(1)请参照小明的计算方法,求乙射击成绩的平均数与方差;
(2)请你从平均数和方差的角度进行分析,谁将被选中。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com