小明在黑板上抄了一道数学题:4(4x-□)=9x+16.但空格内数字因笔迹潦草看不清,他记得此题的答案是x=8,请你帮小明算算空格内的数字是________________.

观察下面三个天平,如图7-1.请在空格内填上第三个天平中缺少的重物的图形.___________.

图7-1

用一根长40米的铁丝围成一个长比宽多8米的长方形,则此长方形的长为_________米,宽为_________米.

若x=2是关于x的方程2x+3k-1=0的解,则k的值是________________.

当x=_____________时,2(x+3)的值与3(1-x)的值互为相反数.

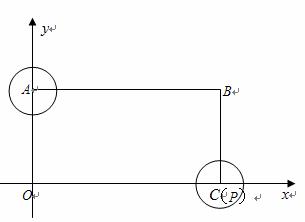
如图，在平面直角坐标系中有一矩形ABCO，B点的坐标为（12，6），点C、A在坐标轴上．⊙A 、⊙P的半径均为1，点P从点C开始在线段CO上以1单位/秒的速度向左运动，运动到点O处停止．与此同时，⊙A的半径每秒钟增大2个单位，当点P停止运动时，⊙A的半径也停止变化．设点P运动的时间为t秒．

（1）在0＜t＜12时，设△OAP的面积为s，试求s与t的函数关系式．并求出当t为何值时，s为矩形ABCO面积的；

（2）在点P的运动过程中，是否存在某一时刻，⊙A 与⊙P相切，若存在求出点P的坐标，若不存在，说明理由．

阅读以下材料：

若关于的三次方程（、、为整数）有整数解，则将代入方程得：    

     ∴

 ∵、、都是整数    ∴是整数    ∴是的因数．

上述过程说明：整数系数方程的整数解只能是常数项的因数．如：∵方程中常数项－2的因数为：±1和±2，∴将±1和±2分别代入方程得：=－2是该方程的整数解，－1、1、2不是方程的整数解．

解决下列问题：

（1）根据上面的学习，方程的整数解可能          ；

（2）方程有整数解吗？若有，求出整数解；若没有，说明理由．

O点是△ABC所在平面内一动点，连接OB、OC, 并将AB、OB、OC、AC的中点D、E、F、G依次连接，设DEFG能构成四边形.

（1）如图，当O点在△ABC内时，求证：四边形DEFG时平行四边形.

（2）当O点移动到△ABC外时，（1）中的结论是否成立？画出图形并说明理由.

（3）若四边形DEFG为矩形，则O点所在位置应满足什么条件？试说明理由.

问题：如图1，在等边三角形ABC内有一点P，且PA=2， PB=， PC=1．求∠BPC度数的大小和等边三角形ABC的边长．

李明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形（如图2）．连接PP′，可得△P′PB是等边三角形，而△PP′A又是直角三角形（由勾股定理的逆定理可证）．所以∠BP′A=150°，而∠BPC=∠BP′A=150°．进而求出等边△ABC的边长为．问题得到解决．

请你参考李明同学的思路，探究并解决下列问题：如图3，在正方形ABCD内有一点P，且PA=，BP=，PC=1．求∠BPC度数的大小和正方形ABCD的边长．

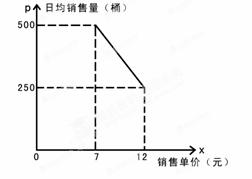
某桶装水经营部每天的房租、人员工资等固定成本为250元，每桶水的进价是5元，规定销售单价不得高于12元/桶，也不得低于7元/桶，调查发现日均销售量p(桶)与销售单价x（元）的函数图象如图所示．

（1）求日均销售量p（桶）与销售单价x（元）的函数关系；

（2）若该经营部希望日均获利1350元，请你根据以上信息，就该桶装水的销售单价或销售数量，提出一个用一元二次方程解决的问题，并写出解答过程．