
科目: 来源: 题型:
如图,已知一次函数y1=kx+b与反比例函数![]() 的图象交于A(2,4)、B(﹣4,n)两点.
的图象交于A(2,4)、B(﹣4,n)两点.

(1)分别求出y1和y2的解析式;
(2)写出y1=y2时,x的值;
(3)写出y1>y2时,x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
青海新闻网讯:西宁市为加大向国家环境保护模范城市大步迈进的步伐,积极推进城市绿地、主题公园、休闲场地建设.园林局利用甲种花卉和乙种花卉搭配成A、B两种园艺造型摆放在夏都大道两侧.搭配数量如下表所示:
| 甲种花卉(盆) | 乙种花卉(盆) | |
| A种园艺造型(个) |
|
|
| B种园艺造型(个) |
|
|
(1)已知搭配一个A种园艺造型和一个B种园艺造型共需![]() 元.若园林局搭配A种园艺造型
元.若园林局搭配A种园艺造型![]() 个,B种园艺造型
个,B种园艺造型![]() 个共投入
个共投入![]() 元.则A、B两种园艺 造型的单价分别是多少元?
元.则A、B两种园艺 造型的单价分别是多少元?
(2)如果搭配A、B![]() 两种园艺造型共
两种园艺造型共![]() 个,某校学生课外小组承接了搭配方案的设计,其中甲种花卉不超过
个,某校学生课外小组承接了搭配方案的设计,其中甲种花卉不超过![]() 盆,乙种花卉不超过
盆,乙种花卉不超过![]() 盆,问符合题意的搭配方案有几种?请你帮忙设计出来.
盆,问符合题意的搭配方案有几种?请你帮忙设计出来.
查看答案和解析>>
科目: 来源: 题型:
如图,一次函数![]() 的图象与x轴、y轴分别相交于点A、B.P是射线BO上的一个动点(点P不与点B重合),过点P作PC⊥AB,垂足为C,在射线CA上截取CD=CP,连接PD.设BP=t.
的图象与x轴、y轴分别相交于点A、B.P是射线BO上的一个动点(点P不与点B重合),过点P作PC⊥AB,垂足为C,在射线CA上截取CD=CP,连接PD.设BP=t.

(1)t为何值时,点D恰好与点A重合?
(2)设△PCD与△AOB重叠部分的面积为S,求S与t的函数关系式,并直接写出t的取值范围.
|
查看答案和解析>>
科目: 来源: 题型:阅读理解
阅读材料:若a,b都是非负实数,则![]() .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
证明:∵![]() ,∴
,∴![]() .
.
∴![]() .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立.
举例应用:已知x>0,求函数![]() 的最小值.
的最小值.
解:![]() .当且仅当
.当且仅当![]() ,即x=1时,“=”成立.
,即x=1时,“=”成立.
当x=1时,函数取得最小值,y最小=4.
问题解决:汽车的经济时速是指汽车最省油的行驶速度.某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油![]() 升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
(1)求y关于x的函数关系式(写出自变量x的取值范围);
(2)求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).
查看答案和解析>>
科目: 来源: 题型:
某饮料厂以300千克的A种果汁和240千克的B种果汁为原料,配制生产甲、乙两种新型饮料,已知每千克甲种饮料含0.6千克A种果汁,含0.3千克B种果汁;每千克乙种饮料含0.2千克A种果汁,含0.4千克B种果汁.饮料厂计划生产甲、乙两种新型饮料共650千克,设该厂生产甲种饮料x(千克).
(1)列出满足题意的关于x的不等式组,并求出x的取值范围;
(2)已知该饮料厂的甲种饮料销售价是每1千克3元,乙种饮料销售价是每1千克4元,那么该饮料厂生产甲、乙两种饮料各多少千克,才能使得这批饮料销售总金额最大?
查看答案和解析>>
科目: 来源: 题型:
甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路ι步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行![]() 走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图2.
走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图2.
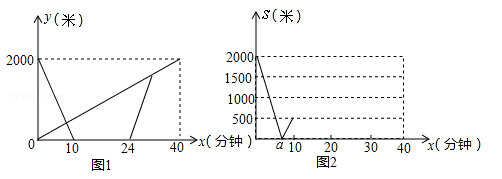
(1)求小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式;
(2)求小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式;
(3)在图2中,补全整个过程中s(米)与x(分钟)之间的函数图象,并确定a的值.
查看答案和解析>>
科目: 来源: 题型:
某工程机械厂根据市场需求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22 400万元,但不超过22 500万元,且所筹资金全部用于生产此两型挖掘机,所生产的此两型挖掘机可全部售出,此两型挖掘机的生![]() 产成本和售价如下表:
产成本和售价如下表:
| 型号 | A | B |
| 成本(万元/台) | 200 | 240 |
| 售价(万元/台) | 250 | 300 |
(1)该厂对这两型挖掘机有哪几种生产方案?
(2)该厂如何生产能获得最大利润?
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂应该如何生产获得最大利润?(注:利润=售价﹣成本)
查看答案和解析>>
科目: 来源: 题型:
某物体从P点运动到Q点所用时间为7秒,其运动速度v(米每秒)关于时间t(秒)的函数关系如图所示.某学习小组经过探究发现:该物体前进3秒运动的路程在数值上等于矩形AODB的面积.由物理学知识还可知:该物体前n(3<n≤7)秒运动的路程在数值上等于矩形AODB的面积与梯形BDNM的面积之和.
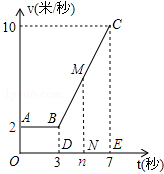
根据以上信息,完成下列问题:
(1)当3<n≤7时,用含t的式子表示v;
(2)分别求该物体在0≤t≤3和3<n≤7时,运动的路程s(米)关于时间t(秒)的函数关系式;并求该物体从P点运动到Q总路程的![]() 时所用的时间.
时所用的时间.
查看答案和解析>>
科目: 来源: 题型:
某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120,具有一次函数的关系,如下表所示.
| x | 50 | 60 | 90 | 120 |
| y | 40 | 38 | 32 | 26 |
(1)求y关于x的函数解析式;
(2)后来在修建的过程中计划发生改变,政府决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.
查看答案和解析>>
科目: 来源: 题型:
某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
| 甲 | 乙 | |
| 进价(元/部) | 4000 | 2500 |
| 售价(元/部) | 4300 | 3000 |
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com