
科目: 来源: 题型:
如图1,在矩形![]() 中,动点
中,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() →
→![]() →
→![]() →
→![]() 方向运动至点
方向运动至点![]() 处停止.设点
处停止.设点![]() 运动的路程为
运动的路程为![]() ,
,![]() 的面积为
的面积为![]() ,如果
,如果![]() 关于
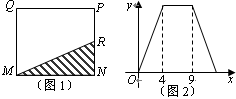
关于![]() 的函数图象如图2所示,则当
的函数图象如图2所示,则当![]() 时,点
时,点![]() 应运
应运![]() 动到
动到
A.![]() 处 B.
处 B.![]() 处 C.
处 C.![]() 处 D.
处 D.![]() 处
处
查看答案和解析>>
科目: 来源: 题型:
如图1,在矩形ABCD中,动点P从点B出发,沿矩形的边由![]() 运动,设点P运动的路程为x,
运动,设点P运动的路程为x,![]() 的面积为y,把y看作x的函数,函数的图像如图2所示,则
的面积为y,把y看作x的函数,函数的图像如图2所示,则![]() 的面积为( )
的面积为( )

A、10 B、16 C、18 D、20
查看答案和解析>>
科目: 来源: 题型:
甲、乙两人在一次百米赛跑中,路程s(米)与赛跑时间t(秒)的关系如图所示,则下列说法正确的是
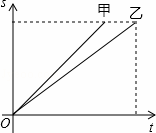
A.甲、乙两人的速度相同 B.甲先到达终点
C.乙用的时间短 D.乙比甲跑的路程多
查看答案和解析>>
科目: 来源: 题型:
为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
| 人均住房面积(平方米) | 单价(万元/平方米) |
| 不超过30(平方米) | 0.3 |
| 超过30平方米不超过m(平方米)部分(45≤m≤60) | 0.5 |
| 超过m平方米部分 | 0.7 |
根据这个购房方案:
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式;
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且57<y≤60 时,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:
| 类型 价格 | 进价(元/盏) | 售价(元/盏) |
| A型 | 30 | 45 |
| B型 | 50 | 70 |
(1)若商场预计进货款为3500元,则这两种台灯各购进多少盏?
(2)若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目: 来源: 题型:
如图,已知双曲线![]() 经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.

(1)求k的值;
(2)若△BCD的面积为12,求直线CD的解析式;
(3)判断AB与CD的位置关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
一农民朋友带了若干千克的土豆进城出售,为了方便,他带了一些零钱备用.按市场售出一些后,又降价出售.售出土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图像回答下列问题:

(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余的土豆售完,这时他手中的钱(含备用的钱)是26元,问他一共带了多少千克的土豆?
查看答案和解析>>
科目: 来源: 题型:
某公司投资700万元购甲、乙两种产品的生产技术和设备后,进行这两种产品加工.已知生产甲种产品每件还需成本费30元,生产乙种产品每件还需成本费20元.经市场调研发现:甲![]() 种产品的销售单价为x(元),年销售量为y(万件),当35≤x<50时,y与x之间的函数关系式为y=20﹣0.2x;当50≤x≤70时,y与x的函数关系式如图所示,乙种产品的销售单价,在25元(含)到45元(含)之间,且年销售量稳定在10万件.物价部门规定这两种产品的销售单价之和为90元.
种产品的销售单价为x(元),年销售量为y(万件),当35≤x<50时,y与x之间的函数关系式为y=20﹣0.2x;当50≤x≤70时,y与x的函数关系式如图所示,乙种产品的销售单价,在25元(含)到45元(含)之间,且年销售量稳定在10万件.物价部门规定这两种产品的销售单价之和为90元.
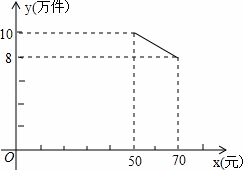
(1)当50≤x≤70时,求出甲种产品的年销售量y(万元)与x(元)之间的函数关系式.
(2)若公司第一年的年销售量利润(年销售利润=年销售收入﹣生产成本)为W(万元),那么怎样定价,可使第一年的年销售利润最大?最大年销售利润是多少?
(3)第二年公司可重新对产品进行定价,在(2)的条件下,并要求甲种产品的销售单价x(元)在50≤x≤70范围内,该公司希望到第二年年底,两年的总盈利(总盈利=两年的年销售利润之和﹣投资成本)不低于85万元.请直接写出第二年乙种产品的销售单价m(元)的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com