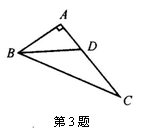
如图所示，在Rt△ABC中，∠A=90°，BD平分∠ABC，交AC于点D，且AB=4，BD=5，则点D到BC的距离是(     ).

   A．3                B．4                C．5                D．6

满足不等式的最小整数是（     ）

   A．－1              B．1               C．2                 D．3

下列语句是命题的是（    ）

   A．作直线AB的平行线                 B．在线段AB上取一点C

C．同角的余角相等                  D．垂线段最短是吗？

在平面直角坐标系中，点P（－1，2）的位置在(     )    

A．第一象限       B．第二象限          C．第三象限          D．第四象限

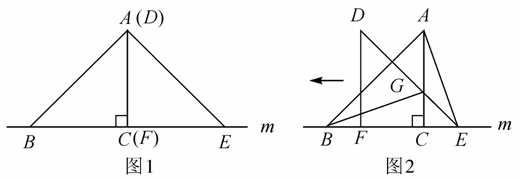
如图，△ABC的边BC在直线m上，AC⊥BC，且AC＝BC，△DEF的边FE也在直线m上，边DF与边AC重合，且DF＝EF.

(1)在图1中，请你通过观察、思考，猜想并写出AB与AE所满足的数量关系和位置关系；(不要求证明)

(2)将△DEF沿直线m向左平移到图2的位置时，DE交AC于点G，连接AE、BG.猜想△BCG与△ACE能否通过旋转重合？请证明你的猜想．

阅读下列材料并解答。

例   平面上有n个点（n≥2）且任意三个点不在同一条直线上，过这些点作直线，一共能作出多少条不同的直线？

（1）分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成3条直线；当有4个点时，可连成6条直线；当有5个点时，可连成10条直线……

（2）归纳：考察点的个数和可连成直线的条数发现：如下表

(3)推理：平面上有n个点，两点确定一条直线。取第一个点A有n种取法，取第二个点B有（n－1）种取法，所以一共可连成n(n-1)条直线，但AB与BA是同一条直线，

故应除以2；即

（4）结论：

试探究以下几个问题：

平面上有n个点（n≥3），任意三个点不在同一条直线上，过任意三个点作三角形，一共能作出多少不同的三角形？

（1）分析：

当仅有3个点时，可作出       个三角形；

    当仅有4个点时，可作出       个三角形；

    当仅有5个点时，可作出       个三角形；

……

（2）归纳：考察点的个数n和可作出的三角形的个数，发现：（填下表）

( 3 ) 推理：                             

（4）结论：

如图所示，在△ABC中，AE⊥AB，AF⊥AC，AE=AB，AF=AC.试判断EC与BF的关系，并说明理由.

已知：如图，锐角△ABC的两条高BD、CE相交于点O，且OB＝OC．

求证：OA平分∠BAC

.

 如图，点A、C、B、D在同一条直线上，AE＝FC，∠A＝∠F，AB＝FD．

求证：BE∥DF

如图，已知∠1=∠2，∠3=∠4. 求证： BD=BC