先阅读下列材料，然后解答问题：

材料1　从3张不同的卡片中选取2张排成一列，有6种不同的排法，抽象成数学问题就是从3个不同元素中选取2个元素的排列，排列数记为A＝3×2＝6.

一般地，从n个不同元素中选取m个元素的排列数记作A，

A＝n(n－1)(n－2)…(n－m＋1)(m≤n)．

例：从5个不同元素中选3个元素排成一列的排列数为：A＝5×4×3＝60.

材料2　从3张不同的卡片中选取2张，有3种不同的选法，抽象成数学问题就是从3个元素中选取2个元素的组合，组合数记为C＝＝3.

一般地，从n个不同元素中选取m个元素的组合数记作C，

C＝(m≤n)．

例：从6个不同元素中选3个元素的组合数为：

C＝＝20.

问：(1)从7个人中选取4人排成一排，有多少种不同的排法？

(2)从某个学习小组8人中选取3人参加活动，有多少种不同的选法？

阅读材料： 小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：3＋2＝(1＋)²，善于思考的小明进行了以下探索：

设a＋b＝(m＋n)²(其中a、b、m、n均为整数)，则有a＋b＝m²＋2n²＋2mn.

∴a＝m²＋2n²，b＝2mn.这样小明就找到了一种把部分a＋b的式子化为平方式的方法．

请你仿照小明的方法探索并解决下列问题：

(1)当a、b、m、n均为正整数时，若a＋b＝(m＋n)²，用含m、n的式子分别表示a、b，得a＝________，b＝________；

(2)利用所探索的结论，找一组正整数a、b、m、n，填空：________＋________＝(______＋______)²；

(3)若a＋4＝(m＋n)²，且a、m、n均为正整数，求a的值．

我们定义＝ad－bc，例如＝2×5－3×4＝10－12＝－2.

若x、y均为整数，且满足1＜＜3，则x＋y的值是________．

若自然数n使得作竖式加法n＋(n＋1)＋(n＋2)均不产生进位现象，则称n为“可连数”，例如32是“可连数”，因为32＋33＋34不产生进位现象；23不是“可连数”，因为23＋24＋25产生了进位现象，那么小于200的“可连数”的个数为________．

数学的美无处不在．数学家们研究发现，弹拨琴弦发出声音的音调高低，取决于弦的长度，绷得一样紧的几根弦，如果长度的比能够表示成整数的比，发出的声音就比较和谐．例如，三根弦长度之比是15∶12∶10，把它们绷得一样紧，用同样的力弹拨，它们将分别发出很调和的乐声do、mi、so.研究15、12、10这三个数的倒数发现：－＝－.我们称15、12、10这三个数为一组调和数．现有一组调和数：x、5、3(x>5)，则x的值是________．

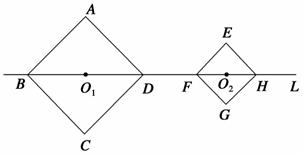
如图，正方形ABCD和正方形EFGH的边长分别为2和，对角线BD、FH都在直线L上，O₁、O₂分别是正方形的中心，线段O₁O₂的长叫做两个正方形的中心距。当中心O₂在直线L上平移时，正方形EFGH也随平移，在平移时正方形EFGH的形状、大小没有改变．

(1)计算：O₁D＝________，O₂F＝________．

(2)当中心O₂在直线L上平移到两个正方形只有一个公共点时，中心距O₁O₂＝________．

(3)随着中心O₂在直线L上的平移，两个正方形的公共点的个数还有哪些变化？并求出相对应的中心距的值或取值范围(不必写出计算过程)．

定义新运算“⊗”，a⊗b＝a－4b，则12⊗(－1)＝________．

阅读下列文字与例题：

将一个多项式分组后，可提公因式或运用公式继续分解的方法是分组分解法．

例如：(1)am＋an＋bm＋bn

＝(am＋bm)＋(an＋bn)

＝m(a＋b)＋n(a＋b)

＝(a＋b)(m＋n)

(2)x²－y²－2y－1

＝x²－(y²＋2y＋1)

＝x²－(y＋1)²

＝(x＋y＋1)(x－y－1)

试用上述方法分解因式a²＋2ab＋ac＋bc＋b².

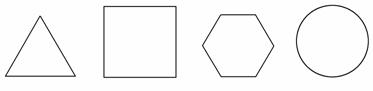
.一个平面封闭图形内(含边界)任意两点距离的最大值称为该图形的“直径”，封闭图形的周长与直径之比称为图形的“周率”，下面四个平面图形(依次为正三角形、正方形、正六边形、圆)的周率从左到右依次记为a₁，a₂，a₃，a₄，则下列关系中正确的是                                               (　　)

A．a₄＞a₂＞a₁                 B．a₄＞a₃＞a₂

C．a₁＞a₂＞a₃                 D．a₂＞a₃＞a₄

已知点A(1，2)和B(－2，5)，试求出两个二次函数，使它们的图象都经过A、B两点．