
科目: 来源:2011年广东省深圳市南山区初二期末数学卷 题型:解答题
阅读下面的例题:
解方程X2-∣X∣-2=0
解:(1)当x≥0时,原方程化为X2-X-2=0,解得X1=2,X2=-1(不合题意,舍去).
(2)当X﹤0时,原方程化为X2+X-2=0,解得X1=1(不合题意,舍去),X2=-2.
∴原方程的根是X1=2,X2=-2.
请参照例题解方程X2-∣X-1∣-1=0.
查看答案和解析>>
科目: 来源:2010年湖北省黄冈市初二上学期期末数学卷 题型:解答题
(1)探究下表中的奥秘,并完成填空:
| 一元二次方程 | 根 | 二次三项式 |
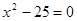 |  | 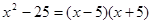 |
 | 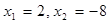 | 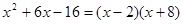 |
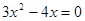 | ________________ |  |
 | 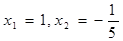 |  |
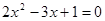 | _________________ | 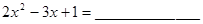 |
 (其中
(其中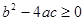 )进行分解?
)进行分解?查看答案和解析>>
科目: 来源:2010年广东省天河区初二上学期期末数学卷doc 题型:解答题
(12分) 阅读并解答问题
用配方法可以解一元二次方程,还可以用它来解决很多问题.例如:因为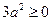 ,所以
,所以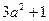 就有最小值1,即
就有最小值1,即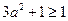 ,只有当
,只有当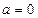 时,才能得到这个式子的最小值1.同样,因为
时,才能得到这个式子的最小值1.同样,因为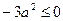 ,所以
,所以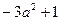 有最大值1,即
有最大值1,即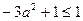 ,只有在
,只有在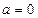 时,才能得到这个式子的最大值1.
时,才能得到这个式子的最大值1.
(1)当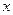 = 时,代数式
= 时,代数式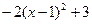 有最 (填写大或小)值为 .
有最 (填写大或小)值为 .
(2)当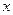 = 时,代数式
= 时,代数式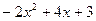 有最 (填写大或小)值为 .
有最 (填写大或小)值为 .
(3)矩形花园的一面靠墙,另外三面的栅栏所围成的总长度是16m,当花园与墙相邻的边长为多少时,花园的面积最大?最大面积是多少?
查看答案和解析>>
科目: 来源:2010年广东省天河区初二上学期期末数学卷doc 题型:解答题
(8分)
已知关于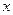 的方程
的方程 .
.
①当m取何值时方程有两个相等的实数根.
②为m选取一个适当的整数,使方程有两个不相等的实数根,并求出这两个实数根
查看答案和解析>>
科目: 来源:2011届湖北省武汉市初三上学期调考测试数学卷doc 题型:解答题
已知关于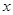 的一元二次方程
的一元二次方程 有实数根,
有实数根, 为正整数.
为正整数.
(1)求 的值;
的值;
(2)当此方程有两个非零的整数根时,求出这两个整数根
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com