
科目: 来源:2012届安徽黄山四校九年级第一阶段联考数学试卷(带解析) 题型:解答题
随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加。据统计,某小区2008年底拥有家庭轿车64辆,2010年底家庭轿车的拥有量达到100辆。
(1) 若该小区2008年底2010年底家庭轿车拥有量的年平均增长率都相同,按2010年的增长率求该小区到2011年底家庭轿车将达到多少辆?
(2) 为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位,据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案。
查看答案和解析>>
科目: 来源:2012-2013学年浙江萧山瓜沥二中八年级上期初摸底检测数学试卷(带解析) 题型:解答题
某市对电话费作了调整,原市话费为:每3分钟0.2元(不足3分钟按3分钟计算);现调整为:前3分钟为0.2元,以后每分钟加收0.1(不足1分钟按1分钟计算).设通话时间x分钟时,调整前话费为a元,调整后话费为b元.
⑴ 填写下表
| x | 4 | 4.2 | 5.8 | 6.3 | 7.1 | 11 |
| a | | | | | | |
| b | | | | | | |
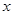 取何值时,
取何值时,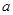 不超过
不超过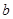 ;(直接写出答案,不需要解答过程)
;(直接写出答案,不需要解答过程)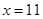 时,请你按调整后的收费方法设计两种通话方案(可以分几次拨打),使所需话费
时,请你按调整后的收费方法设计两种通话方案(可以分几次拨打),使所需话费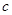 满足关系式:
满足关系式: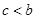 .
.查看答案和解析>>
科目: 来源:2011-2012学年湖北天门七年级下学期期末考试数学试卷(带解析) 题型:解答题
某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元.
(1)若该超市同时一次购进甲、乙两种商品共80件,恰好用去1600元,求能购进甲、乙两种商品各多少件?
(2)若该超市为使甲、乙两种商品共80件的总利润(利润=售价-进价)不少于600元,但又不超过610元,请你帮助该超市设计相应的进货方案.
查看答案和解析>>
科目: 来源:2012届山东淄博恒台县毕业班复习质量检测数学试卷(带解析) 题型:解答题
为了促进长三角区域的便捷沟通,实现节时、节能,杭州湾跨海大桥于2008年5月1日通车,下表是宁波到上海两条线路的有关数据:
| 线路 | 弯路(宁波—杭州—上海) | 直路(宁波—跨海大桥—上海) |
| 路程 | 316公里 | 196公里 |
| 过路费 | 140元 | 180元 |
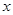 升,汽油价格为5.00元/升,问
升,汽油价格为5.00元/升,问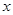 为何值时,走哪条线路的总费用较少(总费用=过路费+油耗费);
为何值时,走哪条线路的总费用较少(总费用=过路费+油耗费);查看答案和解析>>
科目: 来源:2012届山东淄博恒台县毕业班复习质量检测数学试卷(带解析) 题型:解答题
2008年6月1日起,某超市开始有偿提供可重复使用的三种环保购物袋,每只分别为1元、2元和3元,这三种环保购物袋每只最多分别能装大米3公斤、5公斤和8公斤。6月7日,小星和爸爸在该超市选购了3只环保购物袋用来装刚买的20公斤散装大米,他们选购的3只环保购物袋至少应付给超市 元。
查看答案和解析>>
科目: 来源:2011-2012学年陕西西安庆安中学八年级下学期期中考试数学试卷(带解析) 题型:解答题
某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品,共50件,已知生产一件A种产品,需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品,需用甲种原料4千克、乙种原料10千克,可获利润1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你给设计出来;
(2)设生产A、B两种产品获总利润是y(元),其中A种的生产件数是x,试写出y与x之间的函数关系式,并利用函数的性质说明(1)中的哪种生产方案获总利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com