
科目: 来源:2010-2011学年北京平谷区初三第二学期第二次数学统一练习 题型:解答题
如图,在直角坐标平面内,函数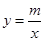 (
(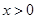 ,
,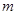 是常数)
是常数)
的图象经过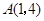 ,
, ,其中
,其中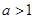 .过点
.过点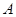 作
作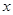 轴垂线,
轴垂线,
垂足为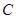 ,过点
,过点 作
作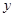 轴垂线,垂足为
轴垂线,垂足为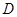 ,连结
,连结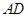 ,
,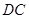 ,
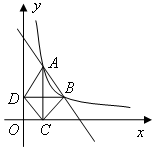
,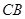 .
.
【小题1】若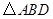 的面积为4,求点
的面积为4,求点 的坐标;
的坐标;
【小题2】若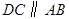 ,当
,当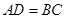 时,求直线
时,求直线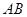 的函数的解析式.
的函数的解析式.
查看答案和解析>>
科目: 来源:2011届安徽省长丰下塘实验中学九年级上学期期中数学卷 题型:解答题
.矩形的长和宽分别是4cm, 3cm ,如果将长和宽都增加x cm ,那么面积增加ycm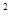
【小题1】求y与x之间的关系式.
【小题2】求当边长增加多少时,面积增加8 cm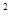
查看答案和解析>>
科目: 来源:2012年河南省中招数学模拟试卷 题型:解答题
随着大陆惠及台胞政策措施的落实,台湾水果进入了大陆市场。一水果经销商购进了A,B两种台湾水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售。预计每箱水果的盈利情况如下表:
有两种配货方案(整箱配货):
方案一:甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱;
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店_________箱,乙店__________箱;B种水果甲店_________箱,乙店__________箱.
【小题1】如果按照方案一配货,请你计算出经销商能盈利多少元?
【小题2】请你将方案二填写完整(只填写一种情况即可),并根据你填写的方案二与方案一作比较,哪种方案盈利较多?
【小题3】在甲、乙两店各配货10箱,且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
查看答案和解析>>
科目: 来源:2011年九年级第一学期期中考试数学卷 题型:解答题
直线y=-x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点匀速出发,同时到达A点时运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动.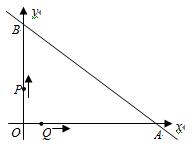
【小题1】直接写出A、B两点的坐标;
【小题2】设点Q的运动时间为t秒,△OPQ的面积为S,求出S与t之间的函数关系式;
【小题3】当s= 时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的
第四个顶点M的坐标.
查看答案和解析>>
科目: 来源:2011年江苏省南京三中八年级第一学期第二次月考数学卷 题型:解答题
一根祝寿蜡烛长85cm,点燃时每小时缩短5cm。
【小题1】请写出点燃后蜡烛的长y(cm)与蜡烛燃烧时间t(h)之间的函数关系式;
【小题2】该蜡烛可点燃多长时间?
查看答案和解析>>
科目: 来源:2010年九年级下学期期末考试数学卷 题型:解答题
如图1,已知抛物线的顶点为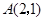 ,且经过原点
,且经过原点 ,与
,与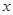 轴的另一个交点为
轴的另一个交点为 .
.
【小题1】求抛物线的解析式;
【小题2】若 点
点 在抛物线的对称轴上,点
在抛物线的对称轴上,点 在抛物线上,且以
在抛物线上,且以 、
、 、
、 、
、 四点为
四点为 顶点的四边形为平行四边形,求
顶点的四边形为平行四边形,求 点的坐标;
点的坐标;
【小题3】连接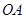 、
、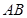 ,如图2,在
,如图2,在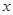 轴下方的抛物线上是否存在点
轴下方的抛物线上是否存在点 ,使得
,使得 与
与 相似?若存在,求出
相似?若存在,求出 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.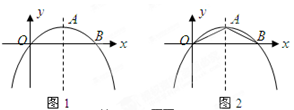
查看答案和解析>>
科目: 来源:2011年河北省衡水市五校九年级下学期第三次月考数学卷 题型:解答题
如图,在平面直角坐标系中,点A、B、C、P的坐标分别为(0,1)、
(-1,0)、(1,0)、(-1,-1)。
【小题1】求经过A、B、C三点的抛物线的表达式;
【小题2】以P为位似中心,将△ABC放大,使得放大后的△A1B1C1与△OAB对应线段的比为3:1,请在右图网格中画出放大后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);
【小题3】经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平移得到?请说明理由。
查看答案和解析>>
科目: 来源:2011年河北省衡水市五校九年级下学期第三次月考数学卷 题型:解答题
深圳大运会期间,某宾馆有若干间住房,住宿记录提供了如下信
息:①7月20日全部住满,一天住宿费收入为3600元;②7月21日有10间房空着,一天住宿费收入为2800元;③该宾馆每间房每天收费标准相同。
【小题1】求该宾馆共有多少间住房,每间住房每天收费多少元?
【小题2】通过市场调查发现,每个住房每天的定价每增加10元,就会有一个房间空闲;己知该宾馆空闲房间每天每间费用10元,有游客居住房间每天每间再增加20元的其他费用,问房价定为多少元时,该宾馆一天的利润最大?
查看答案和解析>>
科目: 来源:2011年九年级下学期第一次月考数学卷 题型:解答题
如图,抛物线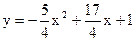 与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
【小题1】求直线AB的函数关系式;
【小题2】动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N. 设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
【小题3】设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由.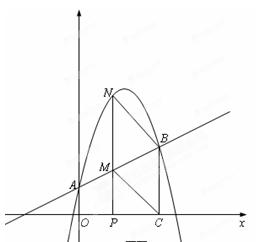
查看答案和解析>>
科目: 来源:2011年九年级下学期第一次月考数学卷 题型:解答题
如图,在平面直角坐标系中有一矩形ABCO,B点的坐标为(12,6),点C、A在坐标轴上.⊙A、⊙P的半径均为1,点P从点C开始在线段CO上以1单位/秒的速度向左运动,运动到点O处停止.与此同时,⊙A的半径每秒钟增大2个单位,当点P停止运动时,⊙A的半径也停止变化.设点P运动的时间为t秒.
【小题1】在0<t<12时,设△OAP的面积为s,试求s与t的函数关系式.并求出当t为何值时,s为矩形ABCO面积的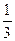 ;
;
【小题2】在点P的运动过程中,是否存在某一时刻,⊙A与⊙P相切,若存在求出点P的坐标,若不存在,说明理由.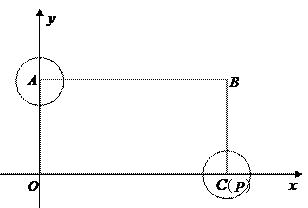
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com