
科目: 来源:2011-2012学年江苏省苏州市工业园区八年级第二学期数学卷 题型:解答题
(6分)已知y=y1 y2,y1与x成正比例,y2与x+3成反比例,当x="0" 时,y=
y2,y1与x成正比例,y2与x+3成反比例,当x="0" 时,y= 2;当x=3时,y=2;求y与x的函数关系式。
2;当x=3时,y=2;求y与x的函数关系式。
查看答案和解析>>
科目: 来源:2011-2012学年山东省济南市实验中学初三模拟考试数学卷 题型:解答题
(本题满分8分)A、B两城间的公路长为450千米,甲、乙两车同时从A城出发沿这一公路驶向B城,甲车到达B城1小时后沿原路返回.如图是它们离A城的路程y(千米)与行驶时间 x(小时)之间的函数图像.
(1)求甲车返回过程中y与x之间的函数解析式,并写出x的取值范围;
(2)乙车行驶6小时与返回的甲车相遇,求乙车的行驶速度.
查看答案和解析>>
科目: 来源:2012届江苏宝应县中考数学模拟试卷 题型:解答题
如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线 //BC,交直线CD于点F.将直线
//BC,交直线CD于点F.将直线 向右平移,设平移距离BE为
向右平移,设平移距离BE为 (t
(t 0),直角梯形ABCD被直线
0),直角梯形ABCD被直线 扫过的面积(图中阴影部份)为S,S关于
扫过的面积(图中阴影部份)为S,S关于 的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
【小题1】梯形上底的长AB=
【小题2】直角梯形ABCD的面积=
【小题3】写出图②中射线NQ表示的实际意义;
【小题4】当 时,求S关于
时,求S关于 的函数关系式;
的函数关系式;
【小题5】当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1: 3.
查看答案和解析>>
科目: 来源:2011-2012学年山东省枣庄市五校12月八年级第一学期单元测试数学卷 题型:解答题
(10分)某人在银行的信用卡存入2万元,每次取出50元,若卡内余额为 y(元),取钱的次数为x.(利息忽略不计)
(1)、写出y与x之间的函数关系式,并求出自变量的取值范围?
(2)、取多少次钱以后,余额为原存款的四分之一?
查看答案和解析>>
科目: 来源:2011-2012学年江苏省启东市东海中学八年级数学寒假测试 题型:解答题
已知y-1与x成正比例,且当x=-1时,y=3.
(1)求y与x的函数解析式;
(2)当y=-7时,求x的值.
查看答案和解析>>
科目: 来源:2012届江苏省姜堰四中全真模拟考试数学试卷 题型:解答题
如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.
【小题1】请用含t的代数式表示出点D的坐标;
【小题2】求t为何值时,△DPA的面积最大,最大为多少
【小题3】在点P从O向A运动的过程中,△DPA 能否成为直角三角形?若能,求t的值.
能否成为直角三角形?若能,求t的值.
若不能,请说明理 由;
由;
【小题4】请直接写出随着点P的运动,点D运动路线的 长.
长.
查看答案和解析>>
科目: 来源:2011-2012学年河南省漯河市龙城一中中考模拟考试数学卷 题型:解答题
直线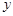 =
=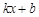 (k≠0)与坐标轴分别交于A、B两点,OA、OB的长分别
(k≠0)与坐标轴分别交于A、B两点,OA、OB的长分别
是方程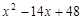 =0的两根(OA>OB).动点P从O点出发,沿路线O→B→A以每
=0的两根(OA>OB).动点P从O点出发,沿路线O→B→A以每
秒1个单位长度的速度运动,到达A点时运动停止.
【小题1】直接写出A、B两点的坐标;
【小题2】设点P的运动时间为t(秒),△OPA的面积为S,求S与t之间的函数关系式;
【小题3】当S=12时,求出点P的坐标,此时,在坐标轴上是否存在点M,使以O、A、
P、M为顶点的四边形是梯形?若存在,请直接写出点M的坐标;若不存在,请说明理由.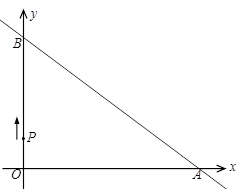
查看答案和解析>>
科目: 来源:2011-2012学年安徽省马鞍山六中中考模拟数学卷 题型:解答题
某蒜薹生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并按这三种方式销售,计划平均每吨的售价及成本如下表:
若经过一段时间,蒜薹按计划全部售出获得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量的 .
.
【小题1】求y与x之间的函数关系式;
【小题2】由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润.
查看答案和解析>>
科目: 来源:2011年浙江省绍兴文理附中九年级下学期第三次月考数学卷 题型:解答题
温州市有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类野生菌在冷库中最多保存160天,同时,平均每天有3千克的野生菌损坏不能出售。
【小题1】设 天后每千克该野生菌的市场价格为
天后每千克该野生菌的市场价格为 元,试写出
元,试写出 与
与 之间的函数关系式;
之间的函数关系式;
【小题2】若存放 天后,将这批野生菌一次性出售,设这批野生菌的销售总额为
天后,将这批野生菌一次性出售,设这批野生菌的销售总额为 元,试写出
元,试写出 与
与 之间的函数关系式;
之间的函数关系式;
【小题3】李经理将这批野生菌存放多少天后出售可获得最大利润 元?
元?
(利润=销售总额-收购成本-各种费用)
查看答案和解析>>
科目: 来源:2011年浙江省桐乡市五校九年级上学期期中考试数学卷 题型:解答题
某超市经销一种销售成本为60元的商品,据超市调查发现,如果按每件70元销售,一周能销售500件,若销售单价每涨1元,每周销售减少10件,设销售价为每件x元(x≥70),一周的销售量为y件.
【小题1】写出y与x的函数关系式(标明x的取值范围).
【小题2】设一周的销售利润为w,写出w与x的函数关系式,并确定当单价在什么范围内变化时,利润随着单价的增大而增大?
【小题3】在超市对该商品投入不超过15000元的情况下,使得一周销售利润达到8000元,销售单价应定为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com