
科目: 来源:2012届浙江湖州中考模拟数学试卷(带解析) 题型:解答题
为改善城市生态环境,实现城市生活垃圾减量化、资源化、无害化的目标,湖州市决定从2010年12月1日起,在全市部分社区试点实施生活垃圾分类处理. 某街道计划建造垃圾初级处理点20个,解决垃圾投放问题. 有A、B两种类型处理点的占地面积、可供使用居民楼幢数及造价见下表:
| 类型 | 占地面积/m2 | 可供使用幢数 | 造价(万元) |
| A | 15 | 18 | 1.5 |
| B | 20 | 30 | 2.1 |
查看答案和解析>>
科目: 来源:2012届湖南衡阳市初中学业水平模拟考试数学卷(带解析) 题型:解答题
我市某西瓜产地组织40辆汽车装运完A、B、C三种西瓜共200吨到外地销售,按计划,40辆汽车都要装运,每辆汽车只能装运同一种西瓜,且必须装满,根据下表提供的信息,解答以下问题: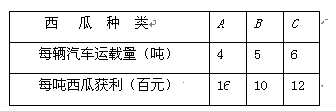
(1)设装运A种西瓜的车数为x,装运B种西瓜的车数为y,求y与x的函数关系式。
(2)如果装运每种西瓜的车辆数都不少于10辆,那么车辆的安排方案有几种?并写出每种安排方案。
(3)若要使此次销售获利达到预期利润25万元,应采取哪样的车辆安排方案?。
查看答案和解析>>
科目: 来源:2011-2012学年重庆市沙坪坝区八年级下学期半期调研测试数学卷(带解析) 题型:解答题
如图①,在矩形ABCD中,AB=l0cm,BC=8cm,点P从A发,沿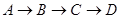 路线运动,到D停止;点
路线运动,到D停止;点 从
从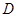 出发,沿
出发,沿 路线运动,到
路线运动,到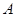 停止.若点
停止.若点
 同时出发,点
同时出发,点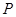 的速度为
的速度为 点
点 的速度为
的速度为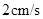 ,
,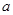 秒时点
秒时点 点
点 同时改变速度,点
同时改变速度,点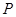 的速度变为bcm/s,点
的速度变为bcm/s,点 的速度变为
的速度变为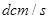 .图②是点
.图②是点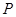 出发x秒后
出发x秒后 的面积
的面积 与
与 的函数关系图象;图③点
的函数关系图象;图③点 出发
出发 秒后
秒后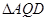 的面积
的面积 的函数关系图象.
的函数关系图象.
(1)观察下图,求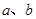 、c的值及点
、c的值及点 的速度
的速度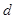 的值;
的值;
(2)设点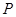 离开点
离开点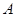 的路程为
的路程为 点
点 到
到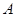 还需走的路程为
还需走的路程为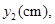 请分别写出动点
请分别写出动点 改变速度后
改变速度后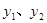 与出发后的运动时间
与出发后的运动时间 的函数关系式,并求出
的函数关系式,并求出 相遇时x的值;
相遇时x的值;
(3)请直接写出当点 出发多少秒时,点
出发多少秒时,点 点
点 在运动路线上相距的路程为25cm.
在运动路线上相距的路程为25cm.
查看答案和解析>>
科目: 来源:2011-2012学年重庆市沙坪坝区八年级下学期半期调研测试数学卷(带解析) 题型:解答题
某商场计划采购甲、乙、丙三种型号的“格力”牌空调共25台.三种型号的空调进价和售价如下表: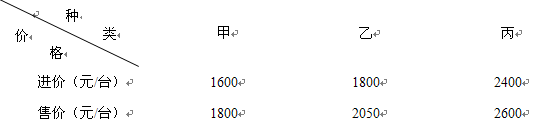
商场计划投入总资金5万元,所购进的甲、丙型号空调数量相同,乙型号数量不超过甲型号数量的一半.若设购买甲型号空调 台,所有型号空调全部售出后获得的总利润为
台,所有型号空调全部售出后获得的总利润为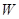 元.
元.
(1)求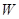 与
与 之间的函数关系式.
之间的函数关系式.
(2)商场如何采购空调才能获得最大利润?
(3)由于原材料上涨,商场决定将丙型号空调的售价提高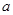 元(
元( ),其余型号售价不变,则商场又该如何采购才能获得最大利润?
),其余型号售价不变,则商场又该如何采购才能获得最大利润?
查看答案和解析>>
科目: 来源:2012届浙江省四校九年级联考数学卷(带解析) 题型:解答题
沿同一条路同时从学校出发到图书馆查阅资料,学校与图书馆的路程是4千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图像回答下列问题:
(1)小聪在图书馆查阅资料的时间为 ▲ 分钟,小聪返回学校的速度为 ▲ 千米/分钟,小明到图书馆的速度为 ▲ 千米/分钟;
(2)请你求出小聪返回学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系式;
(3)当小聪与小明相距不超过 千米时(t≥30),求他们经过的时间t的取值范围
千米时(t≥30),求他们经过的时间t的取值范围
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(河南洛阳卷)数学(带解析) 题型:解答题
某中学计划购买A型和B型课桌凳共200套,经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,,且购买4套A型和6套B型课桌凳共需1820元。
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳的 ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(河南洛阳卷)数学(带解析) 题型:解答题
甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离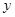 (千米)与
(千米)与 (时间)之间的函数关系图像
(时间)之间的函数关系图像
(1)求甲从B地返回A地的过程中,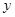 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)若乙出发后2小时和甲相遇,求乙从A地到B地用了多长时间?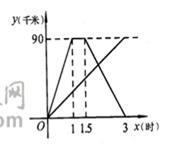
查看答案和解析>>
科目: 来源:2011-2012学年浙江省金华四中九年级毕业生学业考试模拟数学卷(带解析) 题型:解答题
如图1,在等腰梯形ABCO中,AB∥CO,E是AO的中点,过点E作EF∥OC交BC于F,AO=4,OC=6,∠AOC=60°.现把梯形ABCO放置在平面直角坐标系中,使点O与原点重合,OC在x轴正半轴上,点A,B在第一象限内.
(1)求点E的坐标及线段AB的长;
(2)点P为线段EF上的一个动点,过点P作PM⊥EF交OC于点M,过M作MN∥AO交折线ABC于点N,连结PN,设PE=x.△PMN的面积为S.
①求S关于x的函数关系式;
②△PMN的面积是否存在最大值,若不存在,请说明理由.若存在,求出面积的最大值;
(3)另有一直角梯形EDGH(H在EF上,DG落在OC上,∠EDG=90°,且DG=3,HG∥BC.现在开始操作:固定等腰梯形ABCO,将直角梯形EDGH以每秒1个单位的速度沿OC方向向右移动,直到点D与点C重合时停止(如图2).设运动时间为t秒,运动后的直角梯形为E′D′G′H′(如图3);试探究:在运动过程中,等腰梯ABCO与直角梯形E′D′G′H′重合部分的面积y与时间t的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com