
科目: 来源:2010年初中毕业升学考试(浙江台州卷)数学(带解析) 题型:解答题
A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.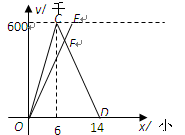
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当它们行驶7了小时时,两车相遇,求乙车速度.
查看答案和解析>>
科目: 来源:2008年初中毕业升学考试(浙江台州卷)数学(带解析) 题型:解答题
在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下: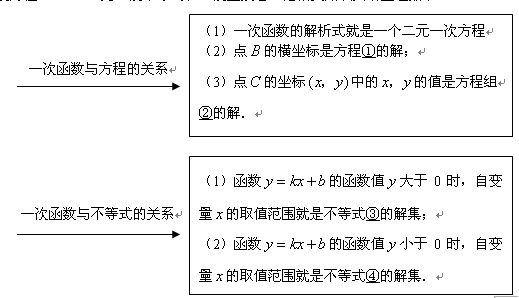
(1)请你根据以上方框中的内容在下面数字序号后写出相应的结论:
① ;② ;③ ;④ ;
(2)如果点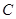 的坐标为
的坐标为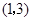 ,那么不等式
,那么不等式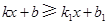 的解集是 .
的解集是 .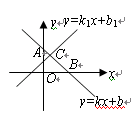
查看答案和解析>>
科目: 来源:2008年初中毕业升学考试(浙江台州卷)数学(带解析) 题型:解答题
如图,一次函数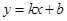 的图象与反比例函数
的图象与反比例函数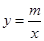 的图象交于
的图象交于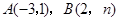 两点,直线
两点,直线 分别交
分别交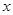 轴、
轴、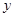 轴于
轴于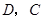 两点.
两点.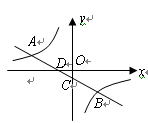
(1)求上述反比例函数和一次函数的解析式;
(2)求 的值.
的值.
查看答案和解析>>
科目: 来源:2008年初中毕业升学考试(黑龙江牡丹江卷)数学(带解析) 题型:解答题
某工厂计划为震区生产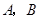 两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套
两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套 型桌椅(一桌两椅)需木料
型桌椅(一桌两椅)需木料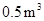 ,一套
,一套 型桌椅(一桌三椅)需木料
型桌椅(一桌三椅)需木料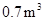 ,工厂现有库存木料
,工厂现有库存木料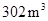 .
.
(1)有多少种生产方案?
(2)现要把生产的全部桌椅运往震区,已知每套 型桌椅的生产成本为100元,运费2元;每套
型桌椅的生产成本为100元,运费2元;每套 型桌椅的生产成本为120元,运费4元,求总费用
型桌椅的生产成本为120元,运费4元,求总费用 (元)与生产
(元)与生产 型桌椅
型桌椅 (套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用
(套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用 生产成本
生产成本 运费)
运费)
(3)按(2)的方案计算,有没有剩余木料?如果有,请直接写出用剩余木料再生产以上两种型号的桌椅,最多还可以为多少名学生提供桌椅;如果没有,请说明理由.
查看答案和解析>>
科目: 来源:2008年初中毕业升学考试(黑龙江牡丹江卷)数学(带解析) 题型:解答题
武警战士乘一冲锋舟从 地逆流而上,前往
地逆流而上,前往 地营救受困群众,途经
地营救受困群众,途经 地时,由所携带的救生艇将
地时,由所携带的救生艇将 地受困群众运回
地受困群众运回 地,冲锋舟继续前进,到
地,冲锋舟继续前进,到 地接到群众后立刻返回
地接到群众后立刻返回 地,途中曾与救生艇相遇.冲锋舟和救生艇距
地,途中曾与救生艇相遇.冲锋舟和救生艇距 地的距离
地的距离 (千米)和冲锋舟出发后所用时间
(千米)和冲锋舟出发后所用时间 (分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
(分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
(1)请直接写出冲锋舟从 地到
地到 地所用的时间.
地所用的时间.
(2)求水流的速度.
(3)冲锋舟将 地群众安全送到
地群众安全送到 地后,又立即去接应救生艇.已知救生艇与
地后,又立即去接应救生艇.已知救生艇与 地的距离
地的距离 (千米)和冲锋舟出发后所用时间
(千米)和冲锋舟出发后所用时间 (分)之间的函数关系式为
(分)之间的函数关系式为 ,假设群众上下船的时间不计,求冲锋舟在距离
,假设群众上下船的时间不计,求冲锋舟在距离 地多远处与救生艇第二次相遇?
地多远处与救生艇第二次相遇?
查看答案和解析>>
科目: 来源:2009年初中毕业升学考试(吉林长春卷)数学(带解析) 题型:解答题
如图,直线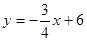 分别与x轴、y轴交于A、B两点;直线
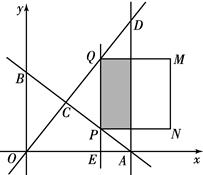
分别与x轴、y轴交于A、B两点;直线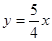 与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
(1)求点C的坐标.
(2)当0<t<5时,求S与t之间的函数关系式.
(3)求(2)中S的最大值.
(4)当t>0时,直接写出点(4,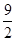 )在正方形PQMN内部时t的取值范围.
)在正方形PQMN内部时t的取值范围.
【参考公式:二次函数y=ax2+bx+c图象的顶点坐标为(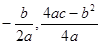 ).】
).】
查看答案和解析>>
科目: 来源:2009年初中毕业升学考试(吉林长春卷)数学(带解析) 题型:解答题
某部队甲、乙两班参加植树活动.乙班先植树30棵,然后甲班才开始与乙班一起植树.设甲班植树的总量为y甲(棵),乙班植树的总量为y乙(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时).y甲、y乙分别与x之间的部分函数图象如图所示.
(1)当0≤x≤6时,分别求y甲、y乙与x之间的函数关系式.
(2)如果甲、乙两班均保持前6个小时的工作效率,通过计算说明,当x=8时,甲、乙两班植树的总量之和能否超过260棵.
(3)如果6个小时后,甲班保持前6个小时的工作效率,乙班通过增加人数,提高了工作效率,这样继续植树2小时,活动结束.当x=8时,两班之间植树的总量相差20棵,求乙班增加人数后平均每小时植树多少棵. 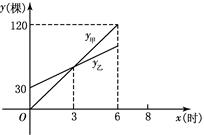
查看答案和解析>>
科目: 来源:2006年初中毕业升学考试(吉林长春卷)数学(带解析) 题型:解答题
小张骑车往返于甲、乙两地,距甲地的路程 (千米)与时间
(千米)与时间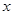 (小时)的函数图象如图所示.
(小时)的函数图象如图所示.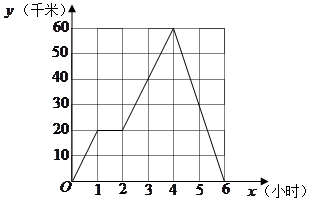
(1)小张在路上停留 小时,他从乙地返回时骑车的速度为 千米/时.(3分)
(2)小李与小张同时从甲地出发,按相同路线匀速前往乙地,到乙地停止,途中小李与小张共相遇3次.请在图中画出小李距甲地的路程 (千米)与时间
(千米)与时间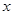 (小时)的函数的大致图象.(3分)
(小时)的函数的大致图象.(3分)
(3)小王与小张同时出发,按相同路线前往乙地,距甲地的路程 (千米)与时间
(千米)与时间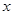 (小时)的函数关系式为
(小时)的函数关系式为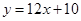 .小王与小张在途中共相遇几次?请你计算第一次相遇的时间.(4分)
.小王与小张在途中共相遇几次?请你计算第一次相遇的时间.(4分)
查看答案和解析>>
科目: 来源:2004年初中毕业升学考试(浙江温州卷)数学(带解析) 题型:解答题
水是生命之源,水资源的不足严重制约我市的工业发展,解决缺水的根本在于节约用水,提高工业用水的重复利用率、降低每万元工业产值的用水量都是有力举措。据《台州日报》4月26日报导,目前,我市工业用水每天只能供应10万吨,重复利用率为45℅,先进地区为75℅,工业每万元产值平均用水25吨,而先进地区为10吨,可见我市节水空间还很大。
(1)若我市工业用水重复利用率(为方便,假设工业用水只重复利用一次)由目前的45℅增加到60℅,那么每天还可以增加多少吨工业用水?
(2)写出工业用水重复利用率由45℅增加到x℅(45<x<100),每天所增加的工业用水y(万吨)与之间的函数关系式。
(3)如果我市工业用水重复利用率及每万元工业产值平均用水量都达到先进地区水平,那么与现有水平比较,仅从用水的角度我市每天能增加多少万元工业产值?
查看答案和解析>>
科目: 来源:2004年初中毕业升学考试(浙江温州卷)数学(带解析) 题型:解答题
已知动点P以每秒2㎝的速度沿图甲的边框按从 的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:
的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:
(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
(3)图甲中的图形面积的多少?
(4)图乙的b是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com