
科目: 来源:2012-2013学年云南省昆明三中、滇池中学八年级下学期期中考试数学试卷(带解析) 题型:解答题
如图,Rt△ABO的顶点A是双曲线y= 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且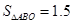 .(1)求这两个函数的解析式;(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.并根据图像写出:(3)方程
.(1)求这两个函数的解析式;(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.并根据图像写出:(3)方程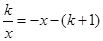 的解;(4)使一次函数的值大于反比例函数的值的
的解;(4)使一次函数的值大于反比例函数的值的 的取值范围;
的取值范围;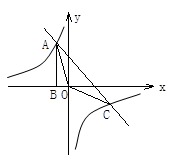
查看答案和解析>>
科目: 来源:2012-2013学年云南省昆明三中、滇池中学八年级下学期期中考试数学试卷(带解析) 题型:解答题
已知一次函数y=ax+b的图像与反比例函数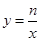 的图像交于A(2,2),B(-1,m),求反比例函数和一次函数的解析式.
的图像交于A(2,2),B(-1,m),求反比例函数和一次函数的解析式.
查看答案和解析>>
科目: 来源:2013年江苏省南京市玄武区中考一模数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,四边形ABCD为矩形,BC平行于x轴,AB=6,点A的横坐标为2,反比例函数y=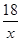 的图像经过点A、C.
的图像经过点A、C.
(1)求点A的坐标;
(2)求经过点A、C所在直线的函数关系式.
(3)请直接写出AD长 .
查看答案和解析>>
科目: 来源:2013年重庆市育才成功学校中考一模数学试卷(带解析) 题型:解答题
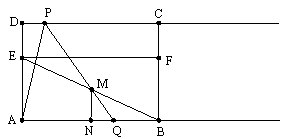
如图,在矩形ABCD中,AB=6,AD=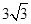 ,点E是AD的三等分点,且AE
,点E是AD的三等分点,且AE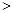 DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为
DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为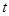 .
.
(1)当点Q与点B重合时,求DP的长度;
(2)设AB的中点为N,PQ与线段BE相交于点M,是否存在点P,使△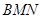 为等腰三角形?若存在,请直接写出时间
为等腰三角形?若存在,请直接写出时间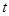 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)设△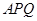 与四边形
与四边形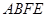 的重叠部分的面积为S,试求S与
的重叠部分的面积为S,试求S与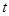 的函数关系式和相应的自变量
的函数关系式和相应的自变量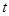 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2013年四川省乐山市沙湾区九年级调研考试数学试卷(带解析) 题型:解答题
如图,某地区对某种药品的需求量 (万件)、供应量
(万件)、供应量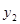 (万件)与价格
(万件)与价格 (元/件)分别近似满足下列函数关系式:
(元/件)分别近似满足下列函数关系式: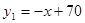 ,
, . 需求量为
. 需求量为 时,即停止供应. 当
时,即停止供应. 当 时,该药品的价格称为稳定价格,需求量称为稳定需求量.
时,该药品的价格称为稳定价格,需求量称为稳定需求量.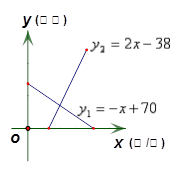
(1)求该药品的稳定价格与稳定需求量;
(2)价格在什么范围内,该药品的需求量低于供应量?
(3)由于该地区突发疫情,政府部门决定对药品供应方提供价格补贴来提高供货价格,以利提高供应量.根据调查统计,需将稳定需求量增加 万件,政府应对每件药品提供多少元补贴,才能使供应量等于需求量.
万件,政府应对每件药品提供多少元补贴,才能使供应量等于需求量.
查看答案和解析>>
科目: 来源:2012-2013学年甘肃省武威第五中学八年级期中考试数学试卷(带解析) 题型:解答题
如图:一次函数y=kx+b的图象与反比例函数y= 的图象相交于A(-2,1)、B(1、n)两点。
的图象相交于A(-2,1)、B(1、n)两点。
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)当x为何值时,一次函数的值大于反比例函数的值?
(直接写出答案)
查看答案和解析>>
科目: 来源:2012-2013学年江苏宿迁青华中学八年级下学期期中检测数学试卷(带解析) 题型:解答题
已知反比例函数y= 与一次函数y=mx+b的图象交于P(-2,1)和Q(1,n)两点.
与一次函数y=mx+b的图象交于P(-2,1)和Q(1,n)两点.
(1)求k、n的值;
(2)求一次函数y=mx+b的解析式;
(3)求△POQ的面积.
查看答案和解析>>
科目: 来源:2013年北京市丰台区中考一模考试数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系xOy中,直线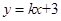 的图象与反比例函数
的图象与反比例函数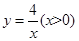 的图象交于点A(1,m),与x轴交于点
的图象交于点A(1,m),与x轴交于点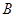 ,过点A作
,过点A作 轴于点
轴于点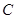 .
.
(1)求一次函数的解析式;
(2)若P为x轴上一点,且△ABP的面积为10,直接写出点 的坐标.
的坐标.
查看答案和解析>>
科目: 来源:2013届江苏省兴化市戴瑶中学九年级一模数学试卷(带解析) 题型:解答题
两城市之间开通了动车组高速列车.已知每隔2 h有一列速度相同的动车组列车从甲城开往乙城.如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象.请根据图中的信息,解答下列问题: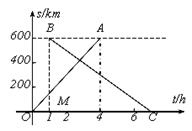
(1)从图象看,普通快车发车时间比第一列动车组列车发车时间 1h(填“早”或“晚”),点B的纵坐标600的实际意义是 ;
(2)请直接在图中画出第二列动车组列车离开甲城的路程s(km)与时间t(h)的函数图象;
(3)若普通快车的速度为100 km/h,
①求BC的表达式,并写出自变量的取值范围;
②第二列动车组列车出发多长时间后与普通快车相遇?
③请直接写出这列普通快车在行驶途中与迎面而来的
相邻两列动车组列车相遇的时间间隔.
查看答案和解析>>
科目: 来源:2013届浙江省杭州市启正中学九年级中考二模(5月)数学试卷(带解析) 题型:解答题
对关于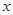 的一次函数
的一次函数 和二次函数
和二次函数 .
.
(1) 当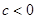 时, 求函数
时, 求函数 的最大值;
的最大值;
(2) 若直线 和抛物线
和抛物线 有且只有一个公共点, 求
有且只有一个公共点, 求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com