
科目: 来源:2010年吉林省长春外国语学校初三上学期第一次月考数学卷 题型:单选题
二次函数y=x2的图象向右平移3个单位,得到新的图象的函数表达式是( )
| A.y=x2+3 | B.y=x2-3 | C.y=(x+3)2 | D.y=(x-3)2 |
查看答案和解析>>
科目: 来源:2010年吉林省长春外国语学校初三上学期第一次月考数学卷 题型:单选题
抛物线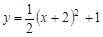 的顶点坐标是( )
的顶点坐标是( )
| A.(2,1) | B.(-2,1) | C.(2,-1) | D.(-2,-1) |
查看答案和解析>>
科目: 来源:2013年初中毕业升学考试(江苏连云港卷)数学(带解析) 题型:解答题
小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
问题情境:如图1,四边形ABCD中,AD∥BC,点E为DC边的中点,连结AE并延长交BC的延长线于点F.求证:S四边形ABCD=S△ABF.(S表示面积)
问题迁移:如图2,在已知锐角∠AOB内有一定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.小明将直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值.请问当直线MN在什么位置时,△MON的面积最小,并说明理由.
实际应用:如图3,若在道路OA、OB之间有一村庄Q发生疫情,防疫部分计划以公路OA、OB和经过防疫站的一条直线MN为隔离线,建立一个面积最小的三角形隔离区△MON.若测得∠AOB=66º,∠POB=30º,OP=4km,试求△MON的面积.(结果精确到0.1km2)(参考数据:sin66º≈0.91,tan66º≈2.25, ≈1.73)
≈1.73)
拓展延伸:如图4,在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)、(6,3)、 、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
查看答案和解析>>
科目: 来源:2012-2013学年山东省乐陵市丁武中学八年级下学期期末考试数学试卷(带解析) 题型:解答题
为预防甲型H1N1流感,某校对教室喷洒药物进行消毒.已知喷洒药物时每立方米空气中的含药量y(毫克)与时间x(分钟)成正比,药物喷洒完后,y与x成反比例(如图所示).现测得10分钟喷洒完后,空气中每立方米的含药量为8毫克.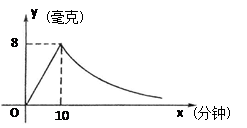
(1)求喷洒药物时和喷洒完后,y关于x的函数关系式;
(2)若空气中每立方米的含药量低于2毫克学生方可进教室,问消毒开始后至少要经过多少分钟,学生才能回到教室?
(3)如果空气中每立方米的含药量不低于4毫克,且持续时间不低于10分钟时,才能杀灭流感病毒,那么此次消毒是否有效?为什么?
查看答案和解析>>
科目: 来源:2012-2013学年山东省乐陵市丁武中学八年级下学期期末考试数学试卷(带解析) 题型:解答题
如图,已知一次函数y=k1x+b的图象与反比例函数y= 的图象交于A(1,-3),B(3,m)两点,连接OA、OB.
的图象交于A(1,-3),B(3,m)两点,连接OA、OB.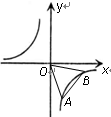
(1)求两个函数的解析式;(2)求△AOB的面积.
查看答案和解析>>
科目: 来源:2013年初中毕业升学考试(湖南常德卷)数学(带解析) 题型:解答题
某地为改善生态环境,积极开展植树造林,甲、乙两人从近几年的统计数据中有如下发现:
(1)求y2与x之间的函数关系式?
(2)若上述关系不变,试计算哪一年该地公益林面积可达防护林面积的2倍?这时该地公益林的面积为多少万亩?
查看答案和解析>>
科目: 来源:2013年初中毕业升学考试(河北卷)数学(带解析) 题型:解答题
如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿轴以每秒1个单位长的速度向上移动,且过点P的直线l: 也随之移动,设移动时间为t秒.
也随之移动,设移动时间为t秒.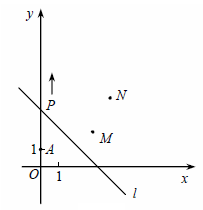
(1)当t=3时,求l的解析式;
(2)若点M,N位于l的异侧,确定t的取值范围;
(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.
查看答案和解析>>
科目: 来源:2012-2013学年黑龙江哈尔滨香坊八年级下学期期末调研测试数学试卷(带解析) 题型:解答题
如图,在平面直角坐标系中,点0为坐标原点,直线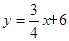 交x轴于点A,交y轴于点B,BD平分∠AB0,点C是x轴的正半轴上一点,连接BC,且AC=AB.
交x轴于点A,交y轴于点B,BD平分∠AB0,点C是x轴的正半轴上一点,连接BC,且AC=AB.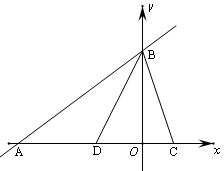
(1)求直线BD的解析式:
(2)过C作CH∥y轴交直线AB于点H,点P是射线CH上的一个动点,过点P作PE⊥CH,直线PE交直线BD于E、交直线BC于F,设线段EF的长为d(d≠0),点P的纵坐标为t,求d与t之间的函数关系式,并写出自变量t的取值范围;
(3)在(2)的条件下,取线段AB的中点M,y轴上有一点N.试问:是否存在这样的t的值,使四边形PEMN是平行四边形,若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2012-2013学年黑龙江哈尔滨香坊八年级下学期期末调研测试数学试卷(带解析) 题型:解答题
加工一种产品,需先将材料加热达到60℃后,再停止加热进行加工,设该材料温度为y﹙℃﹚,从加热开始计算的时间为x(分钟).据了解,该材料在加热时,温度y是时间x的一次函数,停止加热进行加工时,温度y与时间x成反比例关系(如图所示),己知该材料在加热前的温度为l5℃,加热5分钟后温度达到60℃.
(1)分别求出将材料加热和加工时,y与x的函数关系式(不必写出自变量的取值范围);
(2)根据工艺要求,当材料的温度低于l5℃时,必须停止加工,那么加工时间是多少分钟?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com