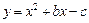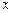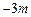已知二次函数的图象与轴两交点的坐标分别为（，0），（，0）（）．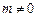
（1）证明；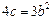
（2）若该函数图象的对称轴为直线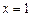，试求二次函数的最小值．

（本小题满分11分）
二次函数的图像如图8所示，请将此图像向右平移1个单位，再向下平移2个单位.
（1）画出经过两次平移后所得到的图像，并写出函数的解析式.
（2）求经过两次平移后的图像与x轴的交点坐标，当x满足什么条件时，函数值大于0？

已知抛物线上有不同的两点E和F．

（1）求抛物线的解析式．
（2）如图，抛物线与x轴和y轴的正半轴分别交于点A和B，M为AB的中点，∠PMQ在AB的同侧以M为中心旋转，且∠PMQ＝45°，MP交y轴于点C，MQ交x轴于点D．设AD的长为m（m＞0），BC的长为n，求n和m之间的函数关系式．
（3）当m，n为何值时，∠PMQ的边过点F．

如图，在水平地面点A处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B．有人在直线AB上点C（靠点B一侧）竖直向上摆放无盖的圆柱形桶，试图让网球落入桶内．已知AB＝4米，AC＝3米，网球飞行最大高度OM=5米，圆柱形桶的直径为0.5米，高为0.3米（网球的体积和圆柱形桶的厚度忽略不计）．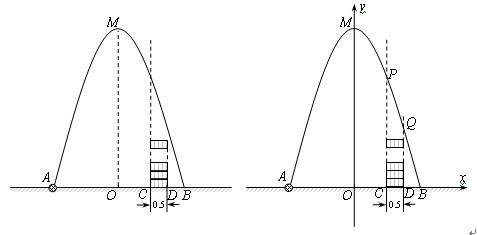

（1）如果竖直摆放5个圆柱形桶时，网球能不能落入桶内？
（2）当竖直摆放圆柱形桶多少个时，网球可以落入桶内？

如图(13.1)，抛物线y＝x2+bx+c与x轴交于A，B两点，与y轴交于点C(0，2)，连接AC，若tan∠OAC＝2．

(1)求抛物线对应的二次函数的解析式；
(2)在抛物线的对称轴l上是否存在点P，使∠APC＝90°，若存在，求出点P的坐标；若不存在，请说明理由；
(3)如图(13.2)所示，连接BC，M是线段BC上(不与B、C重合)的一个动点，过点M作直线l′∥l，交抛物线于点N，连接CN、BN，设点M的横坐标为t．当t为何值时，△BCN的面积最大？最大面积为多少？

（满分13分）如图11，在平面直角坐标系中，直线与轴、轴分别交于点B、C ；抛物线经过B、C两点，并与轴交于另一点A．

（1）求该抛物线所对应的函数关系式；
（2）设是（1）所得抛物线上的一个动点，过点P作直线轴于点M，交直线BC于点N ．
① 若点P在第一象限内．试问：线段PN的长度是否存在最大值 ？若存在，求出它的最大值及此时x的值；若不存在，请说明理由；
② 求以BC为底边的等腰△BPC的面积．

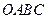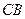如图，在直角梯形中，∥，，点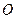为坐标原点，点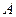在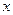轴的正半轴上，对角线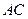，相交于点，，．

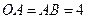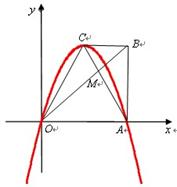
（1）线段的长为           ，点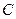的坐标为             ；
（2）求△的面积；
（3）求过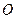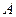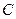，，三点的抛物线的解析式；
（4）若点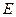在（3）的抛物线的对称轴上，点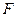为该抛物线上的点，且以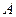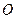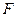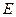，，，四点为顶点的四边形为平行四边形，求点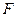的坐标．

如图1，在平面直角坐标系中，拋物线y=ax2+c与x轴正半轴交于点F(16，0)、与y轴正半轴交于点E(0，16)，边长为16的正方形ABCD的顶点D与原点O重合，顶点A与点E重合，顶点C与点F重合；
  
(1) 求拋物线的函数表达式；
(2) 如图2，若正方形ABCD在平面内运动，并且边BC所在的直线始终与x轴垂直，抛物线始终与边AB交于点P且同时与边CD交于点Q(运动时，点P不与A、B两点重合，点Q不与C、D两点重合)。设点A的坐标为(m，n) (m>0)。
j当PO=PF时，分别求出点P和点Q的坐标；
k在j的基础上，当正方形ABCD左右平移时，请直接写出m的取值范围；
l当n=7时，是否存在m的值使点P为AB边中点。若存在，请求出m的值；若不存在，请说明理由。

已知二次函数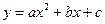的图象经过点A(3，0)，B(2，-3)，C(0，-3)．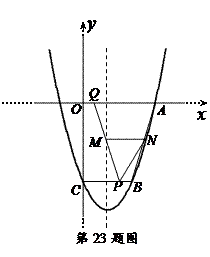

(1)求此函数的解析式及图象的对称轴；
(2)点P从B点出发以每秒0.1个单位的速度沿线段BC向C点运动，点Q从O点出发以相同的速度沿线段OA向A点运动，其中一个动点到达端点时，另一个也随之停止运动．设运动时间为t秒．
①当t为何值时，四边形ABPQ为等腰梯形；
②设PQ与对称轴的交点为M，过M点作x轴的平行线交AB于点N，设四边形ANPQ的面积为S，求面积S关于时间t的函数解析式，并指出t的取值范围；当t为何值时，S有最大值或最小值．

如图，抛物线y = ax² + bx + 4与x轴的两个交点分别为A（－4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．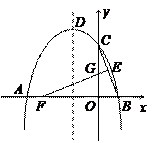

（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；
（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，
△EFK的面积最大？并求出最大面积．