
科目: 来源:2010年高级中等学校招生全国统一考试数学卷(江苏南京) 题型:解答题
已知点A(1,1)在二次函数y=x2-2ax+b的图象上.
(1)用含a的代数式表示b;
(2)如果该二次函数的图象与x轴只有一个交点,求这个二次函数的图象的顶点坐标
查看答案和解析>>
科目: 来源:2010年高级中等学校招生考试数学卷(江苏南通) 题型:解答题
(本题满分9分)
如图,以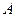 为顶点的抛物线与
为顶点的抛物线与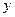 轴交于点
轴交于点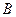 .已知
.已知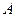 、
、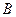 两点坐标分别为(3,0)、(0,4).
两点坐标分别为(3,0)、(0,4).
(1)求抛物线的解析式;
(2)设 是抛物线上的一点(
是抛物线上的一点(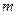 、
、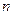 为正整数),且它位于对称轴的右侧.若以
为正整数),且它位于对称轴的右侧.若以 、
、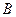 、
、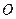 、
、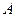 为顶点的四边形四条边的长度是四个连续的正整数,求点
为顶点的四边形四条边的长度是四个连续的正整数,求点 的坐标;
的坐标;
(3)在(2)的条件下,试问:对于抛物线对称轴上的任意一点 ,
,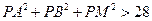 是否总成立?请说明理由.
是否总成立?请说明理由.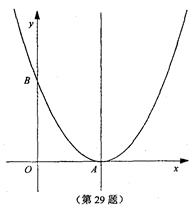
查看答案和解析>>
科目: 来源:2010年高级中等学校招生全国统一考试数学卷(江苏南京) 题型:解答题
如图,二次函数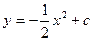 的图象经过点D
的图象经过点D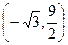 ,与x轴交于A、B两点.
,与x轴交于A、B两点.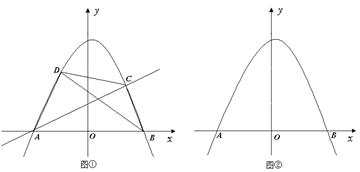
⑴求 的值;
的值;
⑵如图①,设点C为该二次函数的图象在x轴上方的一点,直线AC将四边形ABCD的面积二等分,试证明线段BD被直线AC平分,并求此时直线AC的函数解析式;
⑶设点P、Q为该二次函数的图象在x轴上方的两个动点,试猜想:是否存在这样的点P、Q,使△AQP≌△ABP?如果存在,请举例验证你的猜想;如果不存在,请说明理由.
(图②供选用)
查看答案和解析>>
科目: 来源:2010年高级中等学校招生全国统一考试数学卷(江苏泰州) 题型:解答题
(本小题满分9分)
如图,已知二次函数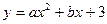 的图象与x轴相交于点A、C,与y轴交于点B,A(
的图象与x轴相交于点A、C,与y轴交于点B,A(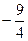 ,0),且△AOB~△BOC。
,0),且△AOB~△BOC。
(1)求C点坐标、∠ABC的度数及二次函数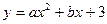 的关系式;
的关系式;
(2)在线段AC上是否存在点M(m,0),使得以线段BM为直径的圆与边BC交于P点(与点B不同),且以点P、C、O为顶点的三角形是等腰三角形?若存在,求出m的值;若不存在,请说明理由
查看答案和解析>>
科目: 来源:2010年高级中等学校招生全国统一考试数学卷(江苏连云港) 题型:解答题
某公司推出一款新型手机,投放市场以来前3个月的利润情况如图所示,该图可以近似看作抛物线的一部分。请结合图象,解答以下问题:
(1)求该抛物线对应的二次函数解析式;
(2)该公司在经营此款手机过程中,第几月的利润能达到24万元?
(3)若照此经营下去,请你结合所学的知识,对公司在此款手机的经营状况(是否亏损?何时亏损?)作预测分析
查看答案和解析>>
科目: 来源:2010年高级中等学校招生全国统一考试数学卷(江苏连云港) 题型:解答题
已知二次函数的解析式为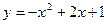 .
.
(1)写这个二次函数图象的对称轴和顶点坐标,并求图象与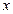 轴的交点坐标;
轴的交点坐标;
(2)在给定的坐标系中画出这个二次函数大致图象,并求出抛物线与坐标轴的交点所组成的三角形的面积
查看答案和解析>>
科目: 来源:2010年高级中等学校招生全国统一考试数学卷(江苏扬州) 题型:解答题
(本小题满分14分)
已知:如图,抛物线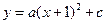 与y轴交于点C(0,
与y轴交于点C(0,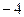 ), 与x轴交于点A、 B,点A的坐标为(2,0).
), 与x轴交于点A、 B,点A的坐标为(2,0).
(1)求该抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PD∥BC,交AC于点D,连接CP.当△CPD的面积最大时,求点P的坐标;
(3)若平行于x轴的动直线 与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(
与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(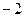 ,0).问:是否存在这样的直线
,0).问:是否存在这样的直线 ,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.
,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2011年广东省中山市初一上学期期末数学卷 题型:解答题
(本小题10分)
抛物线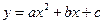 经过点O(0,0),A(4,0),B(2,2).
经过点O(0,0),A(4,0),B(2,2).
(1)求该抛物线的解析式;
(2)画出此抛物线的草图;
(3)求证:△AOB是等腰直角三角形;
(4)将△AOB绕点O按顺时针方向旋转135°得△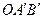 ,写出边
,写出边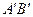 的中点P的 坐标,试判定点P是否在此抛物线上,并说明理由.
的中点P的 坐标,试判定点P是否在此抛物线上,并说明理由.
查看答案和解析>>
科目: 来源:2011届广东省中山市初三上学期期末数学卷doc 题型:解答题
如图①②,在平面直角坐标系中,边长为2的等边△CDE恰好与坐标系中的△OAB重合,现将△CDE绕边AB的中点G(G点也是DE的中点),按顺时针方向旋转180°到△C1DE的位置.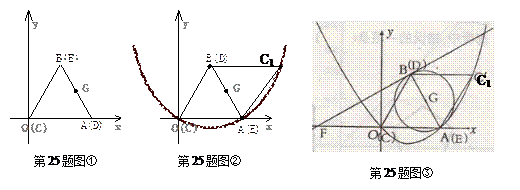
(1)求C1点的坐标;
(2)求经过三点O、A、C1的抛物线的解析式;
(3)如图③,⊙G是以AB为直径的圆,过B点作⊙G的切线与x轴相交于点F,求切线BF
的解析式;
(4)抛物线上是否存在一点M,使得 .若存在,请求出点M的坐标;
.若存在,请求出点M的坐标;
若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2011届广东省中山市初三上学期期末数学卷doc 题型:解答题
某批发市场批发甲、乙两种水果,甲种水果的销售利润 (万元)与进货量
(万元)与进货量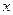 (吨)近似满足函数关系
(吨)近似满足函数关系 ;乙种水果的销售利润
;乙种水果的销售利润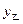 (万元)与进货量
(万元)与进货量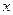 (吨)近似满足函数关系
(吨)近似满足函数关系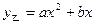 (其中
(其中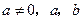 为常数),当
为常数),当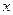 为1吨时,
为1吨时,  为1.4万元;当
为1.4万元;当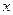 为2吨时,
为2吨时,  为2.6万元.
为2.6万元.
(1)求出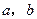 的值,并写出
的值,并写出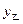 (万元)与
(万元)与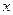 (吨)之间的函数关系式.
(吨)之间的函数关系式.
(2)如果市场准备进甲、乙两种水果共10吨,设乙种水果的进货量为 吨,请你写出这两种水果所获得的销售利润之和
吨,请你写出这两种水果所获得的销售利润之和 (万元)与
(万元)与 (吨)之间的函数关系式,并写出
(吨)之间的函数关系式,并写出 的取值范围。
的取值范围。
(3)在(2)的前提下,这两种水果各进多少吨时,获得的销售利润之和最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com