
科目: 来源:2011年陕西省西安音乐学院初一上学期期末考试数学卷 题型:解答题
如图,已知抛物线与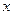 轴交于点
轴交于点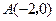 ,
,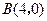 ,与y轴交于点
,与y轴交于点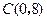 .
.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交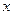 轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
轴于点E.在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由
查看答案和解析>>
科目: 来源:2011年陕西省西安音乐学院初一上学期期末考试数学卷 题型:解答题
随着本区近几年城市建设的快速发展,对花木的需求量逐年提高。某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润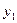 与投资量
与投资量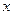 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润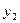 与投资量
与投资量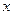 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)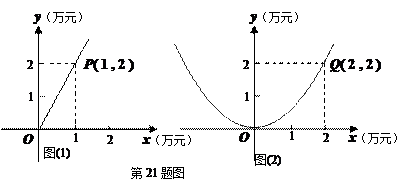
查看答案和解析>>
科目: 来源:2011年陕西省西安音乐学院初一上学期期末考试数学卷 题型:解答题
已知二次函数 的图像经过A(-1,-6)、B(2,-3),求这个函数的解析式及这个函数图像的顶点坐标
的图像经过A(-1,-6)、B(2,-3),求这个函数的解析式及这个函数图像的顶点坐标
查看答案和解析>>
科目: 来源:2011届广东省东莞市教育局教研室初三上学期教学质量自查数学卷 题型:解答题
已知抛物线 经过点A(
经过点A( ,0)、B(m,0)(m>0),且与y轴交于点C.
,0)、B(m,0)(m>0),且与y轴交于点C. 
⑴求a、b的值(用含m的式子表示)
⑵如图所示,⊙M过A、B、C三点,求阴影部分扇形的面积S(用含 m的式子表示);
m的式子表示);
⑶在x轴上方,若抛物线上存在点P,使得以A、B、P为顶点的三角形与 相似,求m的值
相似,求m的值
查看答案和解析>>
科目: 来源:2011年湖南省长沙市长铁一中初一上学期末数学卷 题型:解答题
如图,在平面直角坐标系xOy中, 正方形OABC的边长为2cm, 点A、C分别在y轴的负半轴和x轴的正半轴上, 抛物线y=a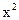 +bx+c经过点A、B,最低点为M,且
+bx+c经过点A、B,最低点为M,且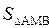 =
=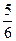
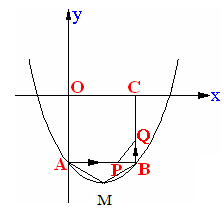
(1)求此抛物线的解析式.,并说明这条抛物线是由抛物线y=a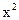 怎样平移得到的。
怎样平移得到的。
(2)如果点P由点A开始沿着射线AB以2cm/s的速度移动, 同时点Q由点B开始沿BC边以1cm/s的速度向点C移动,当其中一点到达终点时运动结束.
①在运动过程中,P、Q两点间的距离是否存在最小值,如果存在,请求出它的最小值。
②当PQ取得最小值时, 在抛物线上是否存在点R, 使得以P、B、Q、R为顶点的四边形是梯形? 如果存在, 求出R点的坐标, 如果不存在, 请说明理由.
查看答案和解析>>
科目: 来源:2011届湖南省岳阳市长炼中学初三上学期末数学卷 题型:解答题
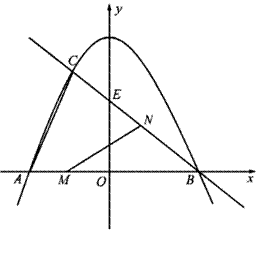
已知:如图,抛物线 与
与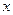 轴交于点
轴交于点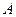 、点
、点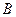 ,与直线
,与直线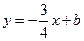 相交于点
相交于点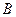 、点
、点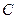 ,直线
,直线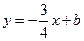 与
与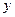 轴交于点
轴交于点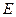 。
。
(1)求直线 的解析式;
的解析式;
(2)求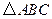 的面积;
的面积;
(3)若点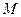 在线段
在线段 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从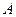 向
向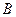 运动(不与
运动(不与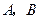 重合),同时,点
重合),同时,点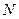 在射线
在射线 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从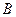 向
向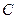 运动.设运动时间为
运动.设运动时间为 秒,请写出
秒,请写出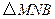 的面积
的面积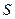 与
与 的函数关系式,并求出点
的函数关系式,并求出点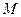 运动多少时间时,
运动多少时间时,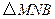 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
查看答案和解析>>
科目: 来源:2011届福建省泉州市洛江区初三上学期期末数学卷 题型:解答题
如图,已知二次函数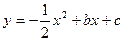 的图象经过A(2,0)、B(0,-6)两点.
的图象经过A(2,0)、B(0,-6)两点.
(1)求这个二次函数的表达式;
(2)设该二次函数的对称轴与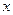 轴交于点C,连结BA、BC,求△ABC的面积
轴交于点C,连结BA、BC,求△ABC的面积
查看答案和解析>>
科目: 来源:2011年福建省晋江市初一上学期末数学卷 题型:解答题
已知抛物线y=ax2+bx+c经过A(-4,3)、B(2,0)两点,当x=3和x=-3时,这条抛物线上对应点的纵坐标相等.经过点C(0,-2)的直线l与 x轴平行,O为坐标原点.
(1)求直线AB和这条抛物线的解析式;
(2)以A为圆心,AO为半径的圆记为⊙A,判断直线l与⊙A的位置关系,并说明理由;
(3)设直线AB上的点D的横坐标为-1,P(m,n)是抛物线y=ax2+bx+c上的动点,当△PDO的周长最小时,求四边形CODP的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com