
科目: 来源:2011年初中毕业升学考试(安徽芜湖卷)数学 题型:解答题
(本小题满分14分)平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别为(0,3)、( ,0),将此平行四边形绕点0顺时针旋转90°,得到平行四边形
,0),将此平行四边形绕点0顺时针旋转90°,得到平行四边形 。
。
(1)若抛物线过点C,A, ,求此抛物线的解析式;
,求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形 重叠部分△
重叠部分△ 的周长;
的周长;
(3)点M是第一象限内抛物线上的一动点,间:点M在何处时△ 的面积最大?最大面积是多少?并求出此时点M的坐标。
的面积最大?最大面积是多少?并求出此时点M的坐标。
查看答案和解析>>
科目: 来源:2011年初中毕业升学考试(贵州遵义卷)数学 题型:解答题
(14分)已知抛物线 经过A(3,0), B(4,1)两点,且与y轴交于点C.
经过A(3,0), B(4,1)两点,且与y轴交于点C.
(1)求抛物线 的函数关系式及点C的坐标;
的函数关系式及点C的坐标;
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求点E的坐标.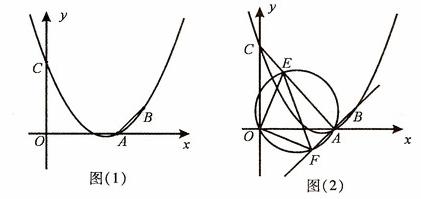
查看答案和解析>>
科目: 来源:2011年江苏省常州市中考数学试卷 题型:解答题
(2011•常州)某商店以6元/千克的价格购进某种干果1140千克,并对其进行筛选分成甲级干果与乙级干果后同时开始销售.这批干果销售结束后,店主从销售统计中发出:甲级干果与乙级干果在销售过程中每天都有销量,且在同一天卖完;甲级干果从开始销售至销售的第x天的总销量y1(千克)与x的关系为y1=﹣x2+40x;乙级干果从开始销售至销售的第t天的总销量y2(千克)与t的关系为y2=at2+bt,且乙级干果的前三天的销售量的情况见下表:
| t | 1 | 2 | 3 |
| y2 | 21 | 44 | 69 |
查看答案和解析>>
科目: 来源:2011年初中毕业升学考试(湖南湘潭卷)数学 题型:解答题
(12分)已知A(1,0)、B(0,-1)、C(-1,2)、D(2,-1)、E(4,2)五个点,抛物线y=a(x-1)2+k(a>0)经过其中的三个点.
(1)求证:C、E两点不可能同时在抛物线y=a(x-1)2+k(a>0)上;
(2)点A在抛物线y=a(x-1)2+k(a>0)上吗?为什么?
(3)求a和k的值.
查看答案和解析>>
科目: 来源:2011年初中毕业升学考试(湖北武汉卷)数学 题型:解答题
(本题满分12分)如图1,抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点.(1)求抛物线的解析式;
(2)设抛物线的顶点为M,直线y=-2x+9与y轴交于点C,与直线OM交于点D.现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)只有一个公共点,求它的顶点横坐标的值或取值范围;
(3)如图2,将抛物线平移,当顶点至原点时,过Q(0,3)作不平行于x轴的直线交抛物线于E,F两点.问在y轴的负半轴上是否存在点P,使△PEF的内心在y轴上.若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2011年初中毕业升学考试(四川成都卷)数学解析版 题型:解答题
(2011•成都)如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
(1)求此抛物线的函数表达式;
(2)设E是y轴右侧抛物线上异于点B的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH.则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)在抛物线上是否存在异于B、C的点M,使△MBC中BC边上的高为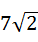 ?若存在,求出点M的坐标;若不存在,请说明理由.
?若存在,求出点M的坐标;若不存在,请说明理由.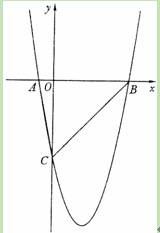
查看答案和解析>>
科目: 来源:2011年初中毕业升学考试(江西卷)数学 题型:解答题
已知:抛物线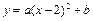
 的顶点为A,与x轴的交点为B,C(点B
的顶点为A,与x轴的交点为B,C(点B
在点C的左侧).
(1)直接写出抛物线对称轴方程;
(2)若抛物线经过原点,且△ABC为直角三角形,求a,b的值;
(3)若D为抛物线对称轴上一点,则以A,B,C,D为顶点的四边形能否为正方形?若能,请写出a,b满足的关系式;若不能,说明理由.
查看答案和解析>>
科目: 来源:2011年初中毕业升学考试(湖北武汉卷)数学 题型:解答题
(14分)如图所示,在平面直角坐标系中,抛物线 经过A(-1,
经过A(-1,
0)、B(0,-5)、C(5,0).
(1)求此抛物线的表达式;
(2)若平行于 轴的直线与此抛物线交于E、F两点,以线段EF为直径的圆与
轴的直线与此抛物线交于E、F两点,以线段EF为直径的圆与 轴相切,
轴相切,
求该圆的半径;
(3)在点B、点C之间的抛物线上有点D,使 的面积最大,求此时点D的坐标及
的面积最大,求此时点D的坐标及
的面积.
查看答案和解析>>
科目: 来源:2011年初中毕业升学考试(四川成都卷)数学解析版 题型:解答题
(2011•舟山)已知直线y=kx+3(k<0)分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒.
(1)当k=﹣1时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).
①直接写出t=1秒时C、Q两点的坐标;
②若以Q、C、A为顶点的三角形与△AOB相似,求t的值.
(2)当 时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),
时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),
①求CD的长;
②设△COD的OC边上的高为h,当t为何值时,h的值最大?
查看答案和解析>>
科目: 来源:2011年初中毕业升学考试(四川成都卷)数学解析版 题型:解答题
(本小题满分12分)如图15,在平面直角坐标系中,点P从原点O出发,沿x轴
向右以每秒1个单位长的速度运动t(t>0)秒,抛物线y=x2+bx+c经过点O和点P.已知
矩形ABCD的三个顶点为A(1,0)、B(1,-5)、D(4,0).
⑴求c、b(用含t的代数式表示);
⑵当4<t<5时,设抛物线分别与线段AB、CD交于点M、N.
①在点P的运动过程中,你认为∠AMP的大小是否会变化?若变化,说明理由;若不变,求出∠AMP的值;
②求△MPN的面积S与t的函数关系式,并求t为何值时,S=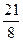 ;
;
③在矩形ABCD的内部(不含边界),把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分,请直接写出t的取值范围.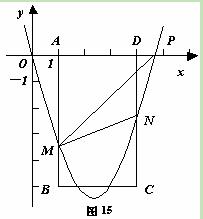
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com