
科目: 来源:2010-2011学年度临沂市费县八年级第二学期期末检测数学 题型:解答题
(11·孝感)(满分14分)如图(1),矩形ABCD的一边BC在直接 坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(
坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(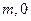 ),其中
),其中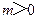 .
.
(1)求点E、F的坐标(用含的式子表示);(5分)
(2)连接OA,若△OAF是等腰三角形,求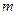 的值;(4分)
的值;(4分)
(3)如图(2),设抛物线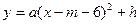 经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求
经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求 、
、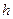 、
、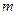 的值.(5分)
的值.(5分)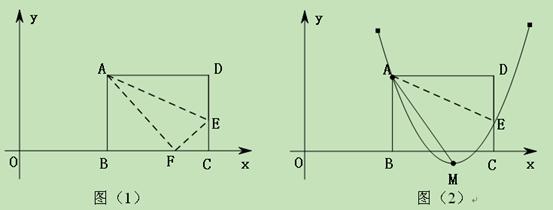
查看答案和解析>>
科目: 来源:2011年初中毕业升学考试(山东济南卷)数学解析版 题型:解答题
(11·十堰)12分)如图,已知抛物线y=x2+bx+c与x轴交于点A(1,0)和点B,与y轴交于点C(0,-3)。
(1)求抛物线的解析式;
(2)如图(1),已知点H(0,-1).问在抛物线上是否存在点G(点G在y轴的左侧),使得S△GHC=S△GHA?若存在,求出点G的坐标,若不存在,请说明理由;
(3)如图(2),抛物线上点D在x轴上的正投影为点E(-2,0),F是OC的中点,连接DF,P为线段BD上的一点,若∠EPF=∠BDF,求线段PE的长.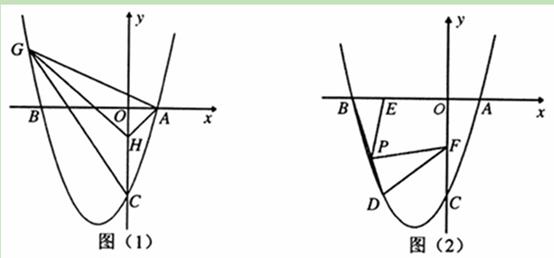
查看答案和解析>>
科目: 来源:2011年初中毕业升学考试(山东济南卷)数学解析版 题型:解答题
(11·丹东)(本题14分)已知:二次函数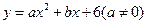 与
与 轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程
轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程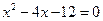 的两个根.
的两个根.
(1)请直接写出点A、点B的坐标.
(2)请求出该二次函数表达式及对称轴和顶点坐标.
(3)如图1,在二次函数对称轴上是否存在点P,使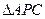 的周长最小,若存在
的周长最小,若存在 ,请求出点P的坐标;若不存在,请说明理由.
,请求出点P的坐标;若不存在,请说明理由.
(4)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合). 过点Q作QD∥AC交于BC点D,设Q点坐标(m,0),当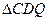 面积S最大时,求m的值.
面积S最大时,求m的值.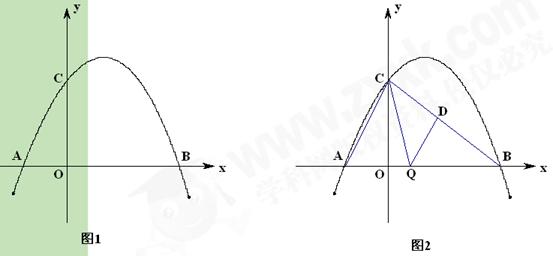
查看答案和解析>>
科目: 来源:2011年初中毕业升学考试(辽宁大连卷)数学 题型:解答题
(11·大连)(本题12分)如图15,抛物线y=ax2+bx+c经过A (-1,0)、B (3,
0)、C (0,3)三点,对称轴与抛物线相交于点P、与直线BC相交于点M,连接PB.
(1)求该抛物线的解析式;
(2)抛物线 上是否存在一点Q,使△QMB与△PMB的面积相等,若存在,求点Q的坐标;
上是否存在一点Q,使△QMB与△PMB的面积相等,若存在,求点Q的坐标;
若不存在,说明理由;
(3)在第一象限、对称轴右侧的抛物线上是否存在一点R,使△RPM与△RMB的面积相
等,若存在,直接写出点R的坐标;若不存在,说明理由.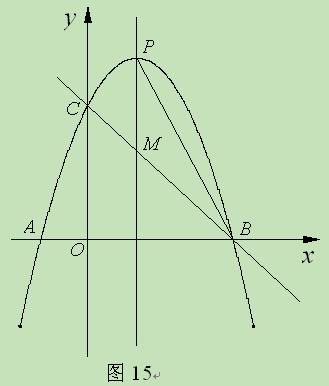
查看答案和解析>>
科目: 来源:2011年滨海新区大港初中毕业生学业考试第一次模拟试卷数学 题型:解答题
(本小题10分)在平面直角坐标系中,将直线l: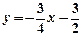 沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线
沿x轴翻折,得到一条新直线与x轴交于点A,与y轴交于点B,将抛物线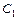 :
: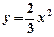 沿x轴平移,得到一条新抛物线
沿x轴平移,得到一条新抛物线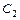 与y轴交于点D,与直线AB交于点E、点F.
与y轴交于点D,与直线AB交于点E、点F.
(Ⅰ)求直线AB的解析式;
(Ⅱ)若线段DF∥x轴,求抛物线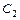 的解析式;
的解析式;
(Ⅲ)在(2)的条件下,若点F在y轴右侧,过F作FH⊥x轴于点G,与直线l交于点H,一条直线m(m不过△AFH的顶点)与AF交于点M,与FH交于点N,如果直线m既垂直于直线AB又平分△AFH的面积,求直线m的解析式.
查看答案和解析>>
科目: 来源:2011年初中毕业升学考试(辽宁大连卷)数学 题型:解答题
(11·天水)(10分)在梯形OABC中,CB∥OA,∠AOC=60°,∠OAB=90°,
OC=2,BC=4,以点O为原点,OA所在的直线为x轴,建立平面直角坐标系,另有一边
长为2的等边△DEF,DE在x轴上(如图(1)),如果让△DEF以每秒1个单位的速度向
左作匀速直线运动,开始时点D与点A重合,当点D到达坐标原点时运动停止.
(1)设△DEF运动时间为t,△DEF与梯形OABC重叠部分的面积为S,求S关于t的函
数关系式.
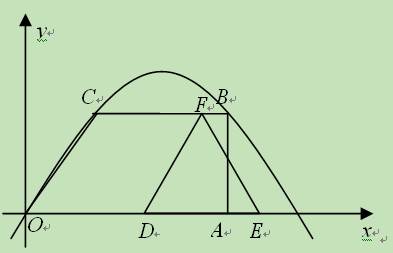
(2)探究:在△DEF运动过程中,如果射线DF交经过O、C、B三点的抛物线于点G,是
否存在这样的时刻t,使得△OAG的面积与梯形OABC的面积相等?若存在,求出t的值;
若不存在,请说明理由.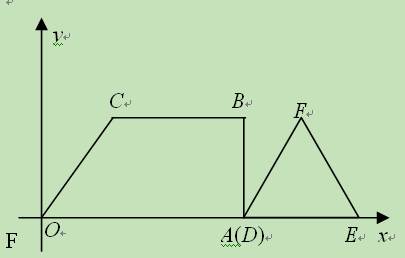
查看答案和解析>>
科目: 来源:2010-2011学年广西灌阳县第二学期期末质量检测七年级数学 题型:解答题
(2011•恩施州)如图,在平面直角坐标系中,直线AC: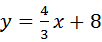 与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c过点A、点C,且与x轴的另一交点为B(x0,0),其中x0>0,又点P是抛物线的对称轴l上一动点.
与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c过点A、点C,且与x轴的另一交点为B(x0,0),其中x0>0,又点P是抛物线的对称轴l上一动点.
(1)求点A的坐标,并在图1中的l上找一点P0,使P0到点A与点C的距离之和最小;
(2)若△PAC周长的最小值为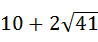 ,求抛物线的解析式及顶点N的坐标;
,求抛物线的解析式及顶点N的坐标;
(3)如图2,在线段CO上有一动点M以每秒2个单位的速度从点C向点O移动(M不与端点C、O重合),过点M作MH∥CB交x轴于点H,设M移动的时间为t秒,试把△P0HM的面积S表示成时间t的函数,当t为何值时,S有最大值,并求出最大值;
(4)在(3)的条件下,当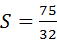 时,过M作x轴的平行线交抛物线于E、F两点,问:
时,过M作x轴的平行线交抛物线于E、F两点,问:
过E、F、C三点的圆与直线CN能否相切于点C?请证明你的结论.(备用图图3)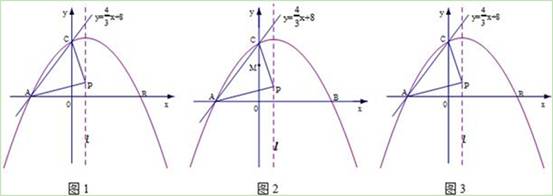
查看答案和解析>>
科目: 来源:2010—2011学年度贵州省贵阳市七年级第二学期期末监测测试题数学 题型:解答题
(2011•广州)已知关于x的二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,点A的坐标是(1,0)
(1)求c的值;
(2)求a的取值范围;
(3)该二次函数的图象与直线y=1交于C、D两点,设A、B、C、D四点构成的四边形的对角线相交于点P,记△PCD的面积为S1,△PAB的面积为S2,当0<a<1时,求证:S1﹣S2为常数,并求出该常数.
查看答案和解析>>
科目: 来源:2010~2011学年度安徽省望江县七年级第二学期期末质量检测数学 题型:解答题
(9分)抛物线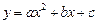 与y轴交于点
与y轴交于点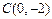 ,与直线
,与直线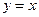
交于点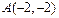 ,
,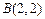 .
.
(1)求抛物线的解析式;
(2)如图,线段MN在线段AB上移动(点M与点A不重合,点N与点B不重合),且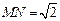 ,若M点的横坐标为m,过点M作
,若M点的横坐标为m,过点M作 x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出m的值;若不能,请说明理由.
x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出m的值;若不能,请说明理由.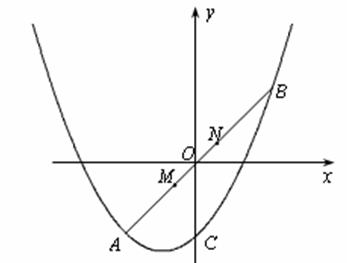
查看答案和解析>>
科目: 来源:2010--2011学年度山东潍坊市四县市七年级第二学期期末质量监测数学 题型:解答题
(11·贺州)(本题满分10分).
如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于
(1)求抛物线的函数表达式;
(2)设抛物线的对称轴 与轴交于点D,试在对称轴上找出点P,使△CDP为等腰三角形,
与轴交于点D,试在对称轴上找出点P,使△CDP为等腰三角形,
请直接写出满足条件的所有点P的坐标.
(3)若点E是线段AB上的一个动点(与A、B不重合),分别连接AC、BC,过点E作EF
∥AC交线段BC于点F,连接CE,记△CEF的面积为S,S是否存在最大值?若存在,求
出S的最大值及此时E点的坐标;若不存在,请说明理由.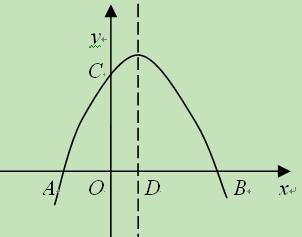
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com