
科目: 来源:2011年山东省桓台县中考二模数学 题型:解答题
(15分)如图,开口向下的抛物线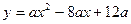 与
与 轴交于
轴交于 、
、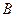 两点,
两点,
抛物线上另有一点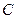 在第一象限,且使
在第一象限,且使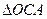 ∽
∽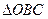 ,(1)求
,(1)求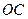 的长及
的长及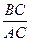 的值;(2)
的值;(2)
设直线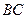 与
与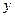 轴交于
轴交于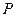 点,点
点,点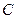 是
是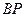 的中点时,求直线
的中点时,求直线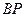 和抛物线的解析式。
和抛物线的解析式。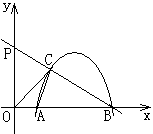
查看答案和解析>>
科目: 来源:2010年黄冈市初中语、数、英三科联赛九年级数学模拟试题C卷 题型:解答题
(本小题满分12分)
为把产品打入国际市场,某企业决定从下面两个投资方案中选择一个进行投资生产.方案一:生产甲产品,每件产品成本为a万美元(a为常数,且3<a<8),每件产品销售价为10万美元,每年最多可生产200件;方案二:生产乙产品,每件产品成本为8万美元,每件产品销售价为18万美元,每年最多可生产120件.另外,年销售x件乙产品时需上交 万美元的特别关税.在不考虑其它因素的情况下:
万美元的特别关税.在不考虑其它因素的情况下:
(1)分别写出该企业两个投资方案的年利润 、
、 与相应生产件数x(x为正整数)之间的函数关系式,并指出自变量的取值范围;
与相应生产件数x(x为正整数)之间的函数关系式,并指出自变量的取值范围;
(2)分别求出这两个投资方案的最大年利润;
(3)如果你是企业决策者,为了获得最大收益,你会选择哪个投资方案?
查看答案和解析>>
科目: 来源:2011届山东省枣庄市第15中学九年级第三次中考模拟考试数学 题型:解答题
(12分)如图,在平面直角坐标系中,已知点A(-2,-4),OB=2,抛物线y
=ax2+bx+c经过点A、O、B三点.
(1)求抛物线的函数表达式;
(2)若点M是抛物线对称轴上一点,试求AM+OM的最小值;
(3)在此抛物线上,是否存在点P,使得以点P与点O、A、B为顶点的四边形是梯形.若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2011年河北省廊坊市广阳区初中毕业生统练一数学 题型:解答题
(本小题满分12分)已知某种水果的批发单价与批发量的函数关系如图1所示.
(1)请说明图中①、②两段函数图象的实际意义.
(2)写出批发 该种水果的资金金额w(元)与
该种水果的资金金额w(元)与 批发量m(kg)之间的函数关系式;在上图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可
批发量m(kg)之间的函数关系式;在上图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可 以批发到较多数量的该种水果.
以批发到较多数量的该种水果.
(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图(2)所示,该经销商以每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.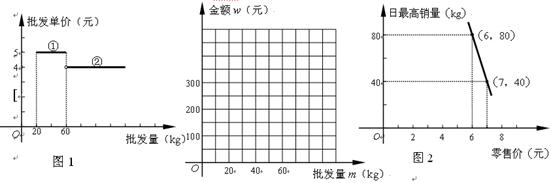
查看答案和解析>>
科目: 来源:2011年初中毕业升学考试(福建泉州卷)数学 题型:解答题
(本小题满分13分)如图,平面直角坐标系中有一直角梯形OMNH,点H的坐
标为(-8,0),点N的坐标为(-6,-4).
(1)画出直角梯形OMNH绕点O旋转180°的图形OABC,并写出顶点A,B,C的坐标(点M的对应点为A,点N的对应点为B,点H的对应点为C);
(2)求出过A,B,C三点的抛物线的表达式;
(3)截取CE=OF=AG=m,且E,F,G分别在线段CO,OA,AB上,求四边形BEFG的面积S与m之间的函数关系式,并写出自变量m的取值范围;面积S是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由;
(4)在(3)的情况下,四边形BEFG是否存在邻边相等的情况,若存在,请直接写出此时m的值,并指出相等的邻边;若不存在,说明理由.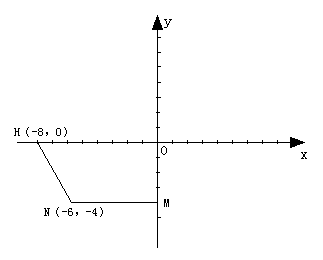
查看答案和解析>>
科目: 来源:2011年初中毕业升学考试(福建泉州卷)数学 题型:解答题
(2011•攀枝花)如图,已知二次函数y=x2+bx+c的图象的对称轴为直线x=1,且与x轴有两个不同的交点,其中一个交点坐标为(﹣1,0).
(1)求二次函数的关系式;
(2)在抛物线上有一点A,其横坐标为﹣2,直线l过点A并绕着点A旋转,与抛物线的另一个交点是点B,点B的横坐标满足﹣2<xB< ,当△AOB的面积最大时,求出此时直线l的关系式;
,当△AOB的面积最大时,求出此时直线l的关系式;
(3)抛物线上是否存在点C使△AOC的面积与(2)中△AOB的最大面积相等.若存在,求出点C的横坐标;若不存在说明理由.
查看答案和解析>>
科目: 来源:2010-2011学年浙江省衢州华茂八年级下学期第二次月考数学试卷 题型:解答题
如图:抛物线 与x 轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C。
与x 轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C。
⑴求抛物线的对称轴和点B的坐标;
⑵过点C作CP⊥对称轴于点P,连结BC交对称轴于点D,连结AC、BP,且  ,求
,求 抛物线的解析式;
抛物线的解析式;
⑶在⑵的条件下,设抛物线的顶点为G,连结BG、CG、求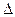 BCG的面积。
BCG的面积。
查看答案和解析>>
科目: 来源:2011年初中毕业升学考试(石家庄桥西区卷)数学 题型:解答题
(2011•雅安)如图,已知二次函数y=ax2+2x+c(a>0)图象的顶点M在反比例函数 上,且与x轴交于AB两点.
上,且与x轴交于AB两点.
(1)若二次函数的对称轴为 ,试求a,c的值;
,试求a,c的值;
(2)在(1)的条件下求AB的长;
(3)若二次函数的对称轴与x轴的交点为N,当NO+MN取最小值时,试求二次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com