
科目: 来源:2011-2012年江苏省张家港市塘桥初级中学九年级第一学期调研试卷数学卷 题型:解答题
(本题2分+4分)已知函数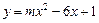 (
(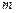 是常数).
是常数).
⑴求证:不论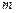 为何值,该函数的图象都经过
为何值,该函数的图象都经过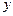 轴上的一个定点;
轴上的一个定点;
⑵若该函数的图象与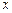 轴只有一个交点,求
轴只有一个交点,求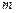 的值.
的值.
查看答案和解析>>
科目: 来源:2011-2012年湖南省长沙市九年级上学期毕业模拟考试(1)数学卷 题型:解答题
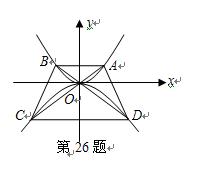
如图,点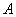 在抛物线
在抛物线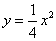 上,过点
上,过点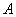 作与
作与 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点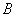 ,延长
,延长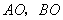 分别与抛物线
分别与抛物线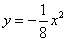 相交于点
相交于点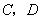 ,连接
,连接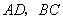 ,设点
,设点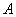 的横坐标为
的横坐标为 ,且
,且 .
.
(1). (4分) 当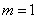 时,求点
时,求点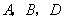 的坐标;
的坐标;
(2). (2分)当 为何值时,四边形
为何值时,四边形 的两条对角线互相垂直;
的两条对角线互相垂直;
(3). (4分) 猜想线段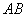 与
与 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
查看答案和解析>>
科目: 来源:2011-2012安徽省当涂县乌溪中学九年级期中测试题数学卷 题型:解答题
(10分)桂林红桥位于桃花江上,是桂林两江四湖的一道亮丽的风景线,该桥的部分横截面 如图所示,上方可看作是一个经过A、C、B三点的抛物线,以桥面的水平线为X轴,经过抛物线的顶点C与X轴垂直的直线为Y轴,建立直
如图所示,上方可看作是一个经过A、C、B三点的抛物线,以桥面的水平线为X轴,经过抛物线的顶点C与X轴垂直的直线为Y轴,建立直 角坐标系,已知此桥垂直于桥面的相邻两柱之间距离为2米(图中用线
角坐标系,已知此桥垂直于桥面的相邻两柱之间距离为2米(图中用线 段AD、CO、BE等表示桥柱)CO=1米,FG=2米
段AD、CO、BE等表示桥柱)CO=1米,FG=2米
(1) 求经过A、B、C三点的抛物线的解析式。
(2) 求柱子AD的高度。
查看答案和解析>>
科目: 来源:2011-2012安徽省当涂县乌溪中学九年级期中测试题数学卷 题型:解答题
(12分)某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间 可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加 元.求:
元.求:
(1)房间每天的入住量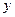 (间)关于
(间)关于 (元)的函数关系式.(3分)
(元)的函数关系式.(3分)
(2)该宾馆每天的房间收费 (元)关于
(元)关于 (元)的函数关系式.(3分)
(元)的函数关系式.(3分)
(3)该宾馆客房部每天的利润 (元)关于
(元)关于 (元)的函数关系式;当每个房间的定价为每天多少元时,
(元)的函数关系式;当每个房间的定价为每天多少元时, 有最大值?最大值是多少?(6分)
有最大值?最大值是多少?(6分)
查看答案和解析>>
科目: 来源:2011-2012安徽省当涂县乌溪中学九年级期中测试题数学卷 题型:解答题
(8分)已知二次函数y=x2-2x-1。
(1) 求此二次函数的图象与x轴的交点坐标.
(2) 将y=x2的图象经过怎样的平移,就可以得到二次函数y=x2-2x -1的图象[来源:Z#xx#k.Co
-1的图象[来源:Z#xx#k.Co
查看答案和解析>>
科目: 来源:2011年安徽省芜湖市九年级模拟试题数学卷 题型:解答题
(本小题满分15分)如图1,抛物线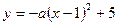 经过点A和点B.已知点A的坐标是(2,4),点B的横坐标是-2.
经过点A和点B.已知点A的坐标是(2,4),点B的横坐标是-2.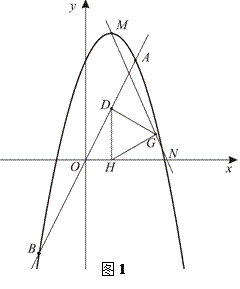
(1)求 的值及点B的坐标;
的值及点B的坐标;
(2)设点D为线段AB上的一个动点,过D作x轴的垂线,垂足为点H.在DH的右侧作等边△DHG. 将过抛物线顶点M的直线记为 ,设
,设 与x轴交于点N.
与x轴交于点N.
① 如图1,当动点D的坐标为(1,2)时,若直线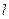 过△DHG的顶点G.求此时点N的横坐标是多少?
过△DHG的顶点G.求此时点N的横坐标是多少?
② 若直线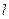 与△DHG的边DG相交,试求点N横坐标的取值范围.
与△DHG的边DG相交,试求点N横坐标的取值范围.
查看答案和解析>>
科目: 来源:2010-2011年山东肥城马埠中学初三模拟试题四数学卷 题型:解答题
(本题11分)如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点O. 为二次函数图象上的一个动点,过点P作
为二次函数图象上的一个动点,过点P作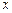 轴的垂线,垂足为D(m,0),并与直线OA交于点C.
轴的垂线,垂足为D(m,0),并与直线OA交于点C.
⑴ 求出二次函数的解析式;
⑵ 当点P在直线OA的上方时,求线段PC的最大值.
⑶ 当 时,探索是否存在点
时,探索是否存在点 ,使得
,使得 为等腰三角形,如果存在,求出
为等腰三角形,如果存在,求出 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源:2011年湖南省长沙市九年级毕业学业考试模拟试卷(四)数学卷 题型:解答题
如图,在平面直角坐标系xOy中,抛物线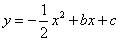 与x轴交于A(1,0)、B(5,0)两点.
与x轴交于A(1,0)、B(5,0)两点.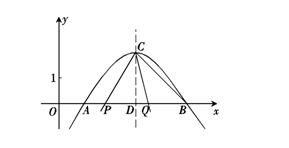
(1). (3分) 求抛物线的解析式和顶点C的坐标;
(2). (7分) 设抛物线的对称轴与x轴交于点D,将∠DCB绕点C按顺时针方向旋转,角的两边CD和CB与x轴分别交于点P、Q,设旋转角为 (0°<
(0°< <90°)
<90°)
①当 等于多少度时,△CPQ是等腰三角形?
等于多少度时,△CPQ是等腰三角形?
②设 ,求s与t之间的函数关系式.
,求s与t之间的函数关系式.
查看答案和解析>>
科目: 来源:2010-2011年厦门外国语学校初三第一学期期中考试数学卷 题型:解答题
(本题12分) 如图,在平面直角坐标系中,二次函数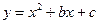 的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.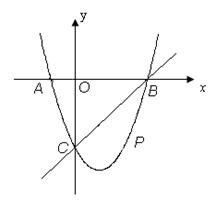
(1)求b,c的值.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形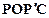 , 那么是否存在点P,使四边形
, 那么是否存在点P,使四边形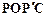 为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目: 来源:2010-2011年厦门外国语学校初三第一学期期中考试数学卷 题型:解答题
(本题10分) 已知一次函数y=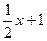 的图象与x轴交于点A.与
的图象与x轴交于点A.与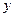 轴交于点
轴交于点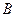 ;二次函数
;二次函数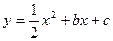 图象与一次函数y=
图象与一次函数y=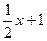 的图象交于
的图象交于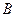 、
、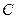 两点,与
两点,与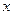 轴交于
轴交于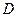 、
、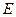 两点且
两点且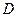 的坐标为
的坐标为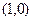
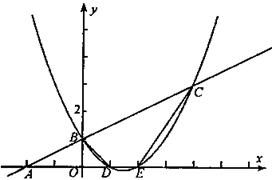
(1)求二次函数的解析式;
(2)在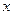 轴上是否存在点P,使得△
轴上是否存在点P,使得△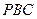 是直角三角形?若存在,求出所有的点
是直角三角形?若存在,求出所有的点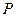 ,若不存在,请说明理由。
,若不存在,请说明理由。
 | |||||
 | |||||
 | |||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com