
科目: 来源:2010年安徽省芜湖市初中毕业学业考试模拟试卷(一)数学卷 题型:解答题
(本小题满分10分)如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于 )的矩形花圃,设花圃一边
)的矩形花圃,设花圃一边 的长为
的长为 m,面积为
m,面积为 .
.
(1)求 与
与 的函数关系式;
的函数关系式;
(2)如果要围成面积为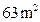 的花圃,
的花圃, 的长是多少?
的长是多少?
(3)能围成面积比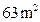 更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
查看答案和解析>>
科目: 来源:2011年湖北省荆州市芦陵中学中考模拟试题(二)数学卷 题型:解答题
(本小题满分12分)如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,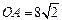 cm, OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒
cm, OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒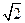 cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
(1)用t的式子表示△OPQ的面积S;
(2)求证:四边形OPBQ的面积是一个定值,并求出这个定值;
(3)当△OPQ与△PAB和△QPB相似时,抛物线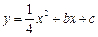 经过B、P两点,过线段BP上一动点M作
经过B、P两点,过线段BP上一动点M作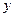 轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.
轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.
查看答案和解析>>
科目: 来源:2011年湖北省荆州市芦陵中学中考模拟试题(二)数学卷 题型:解答题
(10分)恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格10元/千克在我州收购了2000千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存110天,同时,平均每天有6千克的香菇损坏不能出售.
(1)若存放 天后,将这批香菇一次性出售,设这批香菇的销售总金额为
天后,将这批香菇一次性出售,设这批香菇的销售总金额为 元,试写出
元,试写出 与
与 之间的函数关系式.
之间的函数关系式.
(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
查看答案和解析>>
科目: 来源:2010-2011学年江苏省太仓市九年级上学期期中考试数学卷 题型:解答题
(本题9分)
如图,在平面直角坐标系中,抛物线经过A(-1,0),B(3,0),C(0,-1)三点.
(1)求该抛物线的表达式;
(2)点Q在y轴上,点P在抛物线上,要使以点Q、P、A、B为顶点的四边形是平行四边形,求所有满足条件的点P的坐标.
查看答案和解析>>
科目: 来源:2010-2011学年江苏省太仓市九年级上学期期中考试数学卷 题型:解答题
(本题9分)
体育课上,老师训练学生的项目是投篮,假设一名同学投篮后,篮球运行的轨迹是一段抛物线,将所得轨迹形成的抛物线放在如图所示的坐标系中,得到解析式为y=-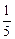 x2+
x2+ x+3.3(单位:m).请你根据所得的解析式,回答下列问题:
x+3.3(单位:m).请你根据所得的解析式,回答下列问题:
(1)球在空中运行的最大高度为多少米?
(2)如果一名学生跳投时,球出手离地面的高度为2.25m,,请问他距篮球筐中心的水平距离是多少?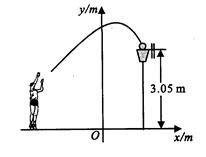
查看答案和解析>>
科目: 来源:2010-2011学年江苏省太仓市九年级上学期期中考试数学卷 题型:解答题
(本题8分)
将二次函数y=2x2-8x-5的图象沿它的对称轴所在直线向上平移,得到一条新的抛物线,这条新的抛物线与直线y=kx+1有一个交点为(3,4).
求:(1)新抛物线的解析式及后的值;
(2)新抛物线与y=kx+1的另一个交点的坐标.
查看答案和解析>>
科目: 来源:2010-2011学年江苏省太仓市九年级上学期期中考试数学卷 题型:解答题
(本题8分)已知二次函数y=- x2+bx+c的图象经过A(2,0),B(0,-6)两点
x2+bx+c的图象经过A(2,0),B(0,-6)两点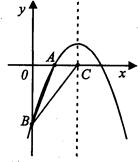
(1)求这个二次函数的解析式;
(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积和周长.
查看答案和解析>>
科目: 来源:2010-2011学年江苏省太仓市九年级上学期期中考试数学卷 题型:解答题
(本题8分)根据条件求下列抛物线的解析式:
(1)二次函数的图象经过(0,1),(2,1)和(3,4);
(2)抛物线的顶点坐标是(-2,1),且经过点(1,-2).
查看答案和解析>>
科目: 来源:2011~2012学年江苏省苏州工业园区九年级上学期期中测试数学卷 题型:解答题
(本题满分10分)已知二次函数y=x2+bx- 3的图像经过点P(-2,5).
3的图像经过点P(-2,5).
(1)求b的值,并写出当0<x≤3时y的取值范围;
(2)设点P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)在这个二次函数的图像上.
①试比较y1和y2的大小;
②当m取不小于5的任意实数时,请你探索:y1、y2、y3能否作为一个三角形
三边的长,并说明理由.
查看答案和解析>>
科目: 来源:2011~2012学年江苏省苏州工业园区九年级上学期期中测试数学卷 题型:解答题
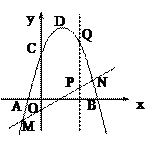
(本题满分9分)如图,在直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交与点A(-1,0)、B(3,0)两点,抛物线交y轴于点C(0,3),点D为抛物线的顶点.直线y=x-1交抛物线于点M、N两点,过线段MN上一点P作y轴的平行线交抛物线于点Q.
(1)求此抛物线的解析式及顶点D的坐标;
(2)问点P在何处时,线段PQ最长,最长为多少?
(3)设E为线段OC上的三等分点,连接EP,EQ,若EP=EQ,求点P的坐标.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com