
科目: 来源:2011-2012年河北省衡水市五校九年级第三次联考数学卷 题型:解答题
(本小题满分9分)深圳大运会期间,某宾馆有若干间住房,住宿记录提供了如下信息:①7月20日全部住满,一天住宿费收入为3600元;②7月21日有10间房空着,一天住宿费收入为2800元;③该宾馆每间房每天收费标准相同。
【小题1】(1)求该宾馆共有多少间住房,每间住房每天收费多少元?
【小题2】(2)通过市场调查发现,每个住房每天的定价每增加10元,就会有一个房间空闲;己知该宾馆空闲房间每天每间费用10元,有游客居住房间每天每间再增加20元的其他费用,问房价定为多少元时,该宾馆一天的利润最大?
查看答案和解析>>
科目: 来源:2011-2012年河北省衡水市五校九年级第三次联考数学卷 题型:解答题
(本小题满分6分)计算:已知二次函数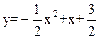 。
。
【小题1】(1)画出图像,指出对称轴,顶点,求出何时y随x的增大而减小;
【小题2】(2)写出不等式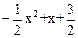 ≥0的解集。
≥0的解集。
查看答案和解析>>
科目: 来源:2011年江苏省宜兴市周铁中学九年级上学期期中考试数学卷 题型:解答题
如图①,有两个形状完全相同的直角三角形ABC和EFG叠放在一起(点A与点E重合),已知AC=8cm,BC=6cm,∠C=90°,EG=4cm,∠EGF=90°,O 是△EFG斜边上的中点.
如图②,若整个△EFG从图①的位置出发,以1cm/s 的速度沿射线AB方向平移,在△EFG 平移的同时,点P从△EFG的顶点G出发,以1cm/s 的速度在直角边GF上向点F运动,当点P到达点F时,点P停止运动,△EFG也随之停止平移.设运动时间为x(s),FG的延长线交 AC于H,四边形OAHP的面积为y(cm2)(不考虑点P与G、F重合的情况).
【小题1】当x为何值时,OP∥AC ?
【小题2】求y与x 之间的函数关系式,并确定自变量x的取值范围.
【小题3】是否存在某一时刻,使四边形OAHP面积与△ABC面积的比为13∶24?若存在,求出x的值;若不存在,说明理由.(参考数据:1142=12996,1152=13225,1162=13456或4.42=19.36,4.52=20.25,4.62=21.16)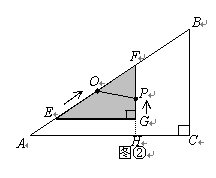

查看答案和解析>>
科目: 来源:2011-2012年湖北省荆州市芦陵中学九年级第二次质检试题数学卷 题型:解答题
(本题满分12分)如图甲,分别以两个彼此相邻的正方形?OABC与CDEF的边OC、OA所在直线为x轴、y轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在x轴上),抛物线y=14x2+bx+c经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
【小题1】(1)求B点坐标;
【小题2】(2)求证:ME是⊙P的切线;
【小题3】(3)设直线AC与抛物线对称轴交于N,Q点是此对称轴上不与N点重合的一动点,①求△ACQ周长的最小值;
②若FQ=t,S△ACQ=S,直接写出S与t之间的函数关系式.
查看答案和解析>>
科目: 来源:2011-2012年湖北省荆州市芦陵中学九年级第二次质检试题数学卷 题型:解答题
(本题满分7分)如图,等腰梯形?ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,求m的值.
查看答案和解析>>
科目: 来源:2011届黑龙江省大庆市三十二中九年级下学期质量检测数学卷 题型:解答题
(本题10分)已知,如图,过点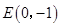 作平行于
作平行于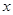 轴的直线
轴的直线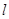 ,抛物线
,抛物线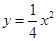 上的两点
上的两点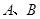 的横坐标分别为
的横坐标分别为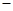 1和4,直线
1和4,直线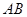 交
交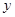 轴于点
轴于点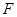 ,过点
,过点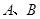 分别作直线
分别作直线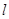 的垂线,垂足分别为点
的垂线,垂足分别为点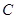 、
、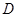 ,连接
,连接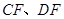 .
.
【小题1】(1)求点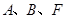 的坐标;
的坐标;
【小题2】(2)求证: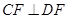 ;
;
【小题3】(3)点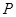 是抛物线
是抛物线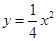 对称轴右侧图象上的一动点,过点
对称轴右侧图象上的一动点,过点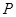 作
作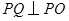 交
交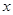 轴于点
轴于点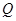 ,是否存在点
,是否存在点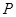 使得
使得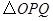 与
与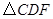 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点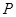 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2011年浙江省杭州西兴中学九年级上学期期中考试数学卷 题型:解答题
(本小题满分12分)
已知二次函数图象的顶点坐标为M(1,0),直线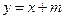 与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在
与该二次函数的图象交于A,B两点,其中A点的坐标为(3,4),B点在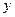 轴上.
轴上.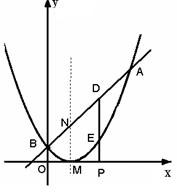
【小题1】(1)求m的值及这个二次函数的解析式;
【小题2】(2)若P(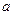 ,0) 是
,0) 是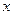 轴上的一个动点,过P作
轴上的一个动点,过P作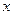 轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
①当0<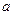 < 3时,求线段DE的最大值;
< 3时,求线段DE的最大值;
②若直线AB与抛物线的对称轴交点为N,
问是否存在一点P,使以M、N、D、E
为顶点的四边形是平行四边形?若存在,
请求出此时P点的坐标;若不存在,请
说明理由.
查看答案和解析>>
科目: 来源:2011年浙江省杭州西兴中学九年级上学期期中考试数学卷 题型:解答题
(本小题满分10分)
设函数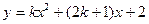 (
(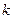 为任意实数)
为任意实数)
【小题1】(1)求证:不论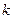 为何值,该函数图象都过点(0,2)和(-2,0);
为何值,该函数图象都过点(0,2)和(-2,0);
【小题2】(2)若该函数图象与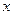 轴只有一个交点,求
轴只有一个交点,求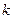 的值.
的值.
查看答案和解析>>
科目: 来源:2011年浙江省杭州西兴中学九年级上学期期中考试数学卷 题型:解答题
(本小题满分6分)
已知抛物线的解析式为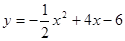
【小题1】(1)求抛物线的顶点坐标;
【小题2】(2)求出抛物线与x轴的交点坐标;
【小题3】(3)当x取何值时y>0?
查看答案和解析>>
科目: 来源:2011年浙江省诸暨市暨阳初中九年级上学期期中考试数学卷 题型:解答题
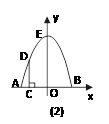
如图(1),某建筑物有一抛物线形的大门,小强想知道这道门的高度. 他先测出门的宽度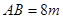 ,然后用一根长为
,然后用一根长为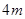 的小竹杆
的小竹杆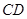 竖直地接触地面和门的内壁,并测得
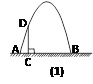
竖直地接触地面和门的内壁,并测得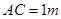 . 小强画出了如图(2)的草图,请你帮他算一算门的高度
. 小强画出了如图(2)的草图,请你帮他算一算门的高度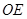 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com