
科目: 来源:2011年安徽省中考压轴题预测试数学卷 题型:解答题
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).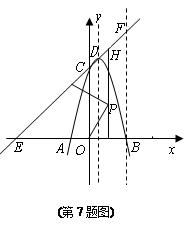
【小题1】求抛物线的解析式及其顶点D的坐标
【小题2】设直线CD交x轴于点E,过点B作x轴的垂线,交直线CD于点F,在坐标平面内找一点G,使以点G、F、C为顶点的三角形与△COE相似,请直接写出符合要求的,并在第一象限的点G的坐标;
【小题3】在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由;
【小题4】将抛物线沿其对称轴平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?
查看答案和解析>>
科目: 来源:2011年安徽省中考压轴题预测试数学卷 题型:解答题
如图,抛物线 交
交 轴于A、B两点(A点在B点左侧),交
轴于A、B两点(A点在B点左侧),交 轴于点C,已知B(8,0),
轴于点C,已知B(8,0), ,△ABC的面积为8.
,△ABC的面积为8.
【小题1】求抛物线的解析式;
【小题2】若动直线EF(EF∥ 轴)从点C开始,以每秒1个长度单位的速度沿
轴)从点C开始,以每秒1个长度单位的速度沿 轴负方向平移,且交
轴负方向平移,且交 轴、线段BC于E、F两点,动点P同时从点B出发,在线段OB上以每秒2个单位的速度向原点O运动。连结FP,设运动时间
轴、线段BC于E、F两点,动点P同时从点B出发,在线段OB上以每秒2个单位的速度向原点O运动。连结FP,设运动时间 秒。当
秒。当 为何值时,
为何值时, 的值最大,并求出最大值;
的值最大,并求出最大值;
【小题3】在满足(2)的条件下,是否存在 的值,使以P、B、F为顶点的三角形与△ABC相似。若存在,试求出
的值,使以P、B、F为顶点的三角形与△ABC相似。若存在,试求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目: 来源:2011年安徽省中考压轴题预测试数学卷 题型:解答题
平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q。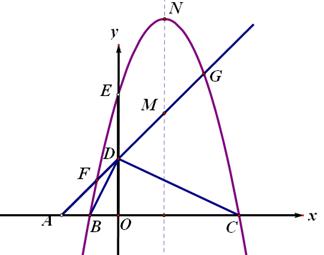
【小题1】求经过B、E、C三点的抛物线的解析式;
【小题2】判断⊿BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标
【小题3】若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由。
查看答案和解析>>
科目: 来源:2011年安徽省中考压轴题预测试数学卷 题型:解答题
如图,在平面直角坐标系xoy中,矩型ABCD的边AB在x轴上,且AB=3,BC=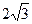 ,直线y=
,直线y=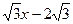 经过点C,交y轴于点G
经过点C,交y轴于点G
【小题1】点C、D的坐标分别是C( ),D( )
【小题2】求顶点在直线y=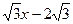 上且经过点C、D的抛物线的解析式
上且经过点C、D的抛物线的解析式
【小题3】将(2)中的抛物线沿直线y=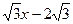 平移,平移后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
平移,平移后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
查看答案和解析>>
科目: 来源:2011-2012年福建省漳州市龙海八中九年级《二次函数》测试数学卷 题型:解答题
某企业投资100万元引进一条产品加工生产线,若不计维修、保养费用,预计投产后每年可创利33万.该生产线投产后,从第1年到第x年的维修、保养费用累计为y(万元),且y=ax2+bx,若第1年的维修、保养费用为2万元,第2年为4万元。
【小题1】(1)求y的解析式;
【小题2】(2)投产后,这个企业在第几年就能收回投资?
查看答案和解析>>
科目: 来源:2011-2012年福建省漳州市龙海八中九年级《二次函数》测试数学卷 题型:解答题
甲车在弯路作刹车试验,收集到的数据如下表所示:
| 速度x(千米/小时) | 0 | 5 | 10 | 15 | 20 |  25 25 | … |
| 刹车距离y(米) | 0 |  | 2 |  | 6 | | … |
 所示的坐标系中画出甲车刹车距离y(米)与
所示的坐标系中画出甲车刹车距离y(米)与 但还是相撞了。事后测得甲、乙两车的刹车距离分别为12米和10.5米,又知乙车的刹车距离y(米)与速度x(千米/时)满足函数
但还是相撞了。事后测得甲、乙两车的刹车距离分别为12米和10.5米,又知乙车的刹车距离y(米)与速度x(千米/时)满足函数 ,请你就两车的速度方面分析相撞的原因。
,请你就两车的速度方面分析相撞的原因。
查看答案和解析>>
科目: 来源:2011-2012年福建省漳州市龙海八中九年级《二次函数》测试数学卷 题型:解答题
有一个抛物线形的桥洞,桥洞离水面的最大高度BM为3米,跨度OA为6米,以OA所在直线为x轴,O为原点建立直角坐标系(如图所示).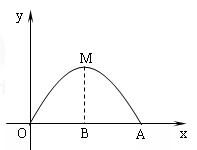
【小题1】⑴请你直接写 出O、A、M三点的坐标;
出O、A、M三点的坐标;
【小题2】⑵一艘小船平放着一些长3米,宽2米且厚度均匀的矩形木板,要使该小船能通过此桥洞,问这些木板最高可堆放多少米
(设船身底板与水面同一平面)?
查看答案和解析>>
科目: 来源:2011-2012年福建省漳州市龙海八中九年级《二次函数》测试数学卷 题型:解答题
已知抛物线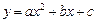 经过(-1,0),(0,-3),(2,-3)三点.
经过(-1,0),(0,-3),(2,-3)三点.
【小题1】⑴求这条抛物线的表达式;
【小题2】⑵写出抛物线的开口方向、对称轴和顶点坐标
查看答案和解析>>
科目: 来源:2011-2012年河北省衡水市五校九年级第三次联考数学卷 题型:解答题
(本小题满分9分)如图,抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点,请解答下列问题: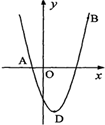
【小题1】(1)求抛物线的解析式;
【小题2】(2)若抛物线的顶点为点D,对称轴所在的直线交x轴于点E,连接AD,点F为AD的中点,求出线段EF的长。注:抛物线y=ax2+bx+c的对称轴是x=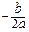 ,顶点坐标是 (
,顶点坐标是 ( ,
,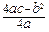 )。
)。
查看答案和解析>>
科目: 来源:2011-2012年河北省衡水市五校九年级第三次联考数学卷 题型:解答题
(本小题满分10分)如图,在平面直角坐标系中,点A、B、C、P的坐标分别为(0,1)、(-1,0)、(1,0)、(-1,-1)。
【小题1】(1)求经过A、B、C三点的抛物线的表达式;
【小题2】(2)以P为位似中心,将△ABC放大,使得放大后的△A1B1C1与△OAB对应线段的比为3:1,请在右图网格中画出放大后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);
【小题3】(3)经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平移得到?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com