
科目: 来源:2011-2012学年云南省昆明八中九年级上学期期中考试数学试卷 题型:解答题
如图,抛物线y=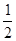 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).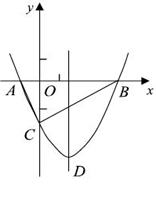
【小题1】求抛物线的解析式及顶点D的坐标
【小题2】判断△ABC的形状,证明你的结论;
【小题3】点M(m,0)是x 轴上的一个动点, 当CM+DM的值最小时,求m的值.
轴上的一个动点, 当CM+DM的值最小时,求m的值.
查看答案和解析>>
科目: 来源:2011-2012浙江省杭州地区九年级第一学期12月月考数学卷 题型:解答题
如图,抛物线 与
与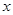 轴交于
轴交于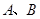 两点,与
两点,与 轴相交于点
轴相交于点 .连结AC、BC,B、C两点的坐标分别为B(1,0)、
.连结AC、BC,B、C两点的坐标分别为B(1,0)、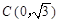 ,且当x=-10和x=8时函数的值
,且当x=-10和x=8时函数的值 相等.
相等.
【小题1】求a、b、c的值;
【小题2】若点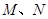 同时从
同时从 点出发,均以每秒1个单位长度的速度分别沿
点出发,均以每秒1个单位长度的速度分别沿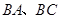 边运动,其中一个点到达终点时,另一点也随之停止运动.连结
边运动,其中一个点到达终点时,另一点也随之停止运动.连结 ,将
,将 沿
沿 翻折,当运动时间为几秒时,
翻折,当运动时间为几秒时, 点恰好落在
点恰好落在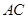 边上的
边上的 处?并求点
处?并求点 的坐标及四边形
的坐标及四边形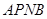 的面积;
的面积;
【小题3】上下平移该抛物线得到新的抛物线,设新抛物线的顶点为D,对称轴与x轴的交点为E,若△ODE与△OBC相似,求新抛物线的解析式。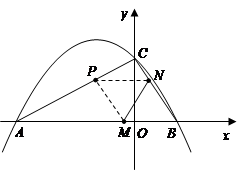
查看答案和解析>>
科目: 来源:2011-2012浙江省杭州地区九年级第一学期12月月考数学卷 题型:解答题
有一种葡萄:从树上摘下后不保鲜最多只能存放一周,如果放在冷藏室,可以延长保鲜时间,但每天仍有一定数量的葡萄变质,假设保鲜期内的重量基本保持不变,现有一位个体户,按市场价收购了这种葡萄200千克放在冷藏室内,此时市场价为每千克2元,据测算,此后每千克鲜葡萄的市场价格每天可以上涨0.2元,但是,存放一天需各种费用20元,平均每天还有1千克葡萄变质丢弃.
【小题1】存放x天后将鲜葡萄一次性出售,设鲜葡萄的销售金额为Y元,写出Y关于x的函数关系式;
【小题2】为了使鲜葡萄的销售金额为760元,又为了尽早清空冷藏室,则需要在几天后一次性出售完;
【小题3】问个体户将这批葡萄存放多少天后一次性出售,可获得最大利润?最大利润是多少?(本题不要求写出自变量x的取值范围)
查看答案和解析>>
科目: 来源:2006-2007年福建省福州市九年级第一学期期末考试数学卷 题型:解答题
(本题满分14分)
如图是某市一条河上一座古拱挢的截面图,拱桥桥洞上沿是抛物线形状,抛物线拱桥处于正常水位时水面宽AB为26m,当水位上涨1m时,抛物线拱桥的水面宽CD为24m.现以水面AB所在直线为x轴,抛物线的对称轴为y轴建立直角坐标系.
【小题1】(1) 求出抛物线的解析式;
【小题2】(2) 经过测算,水面离拱桥顶端1.5m时为警戒水位.某次洪水到来时,小明用仪器测得水面宽为10m,请你帮助小明算一算,此时水面是否超过警戒水位.
查看答案和解析>>
科目: 来源:2010-2011年安徽省长丰县下塘实验中学九年级上学期期中考试数学卷 题型:解答题
(8分) 一元二次方程 的二根
的二根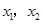 (
(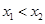 )
)
是抛物线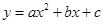 与
与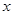 轴的两个交点
轴的两个交点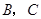 的横坐标,
的横坐标,
且此抛物线过点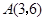 .
.
【小题1】(1)求此二次函数的解析式.
【小题2】(2)用配方法求此抛物线的顶点为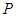 .对称轴
.对称轴
【小题3】(3)当x取什么值时, y随x增大而减小?
查看答案和解析>>
科目: 来源:2010-2011年安徽省长丰县下塘实验中学九年级上学期期中考试数学卷 题型:解答题
(10分)某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
【小题1】(1)求平均每天销售量 (箱)与销售价
(箱)与销售价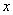 (元
(元 /箱)之间的函数关系式.
/箱)之间的函数关系式.
【小题2】(2)求该批发商平均每天的销售利润 (元)与销售价
(元)与销售价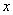 (元/箱)之间的函数关系式.
(元/箱)之间的函数关系式.
【小题3】(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目: 来源:2010-2011年安徽省长丰县下塘实验中学九年级上学期期中考试数学卷 题型:解答题
(6分)矩形的长和宽分别是4cm, 3cm ,如果将长和宽都增加x cm ,那么面积增加ycm
【小题1】(1)求y与x之间的关系式.
【小题2】(2)求当边长增加多少时,面积增加8 cm
查看答案和解析>>
科目: 来源:2011-2012年江苏省盐城市东台富安中学九年级上学期学情调查数学卷 题型:解答题
(本题满分12分)如图,抛物线y=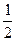 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).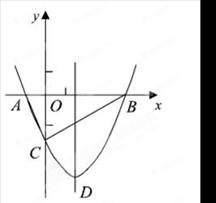
【小题1】⑴求抛物线的解析式及顶点D的坐标;
【小题2】⑵判断△ABC的形状,证明你的结论;
【小题3】⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
查看答案和解析>>
科目: 来源:2011-2012年江苏省盐城市东台富安中学九年级上学期学情调查数学卷 题型:解答题
(本题满分10分)正常水位时,抛物线拱桥下的水面宽为20m,水面上升3m达到该地警戒水位时,桥下水面宽为10m.
【小题1】(1)在恰当的平面直角坐标系中求出水面到桥孔顶部的距离y(m)与水面宽x(m)之间的函数关系式;
【小题2】(2)如果水位以0.2m/h的速度持续上涨,那么达到警戒水位后,再过多长时间此桥孔将被淹没?
查看答案和解析>>
科目: 来源:2011-2012年江苏省盐城市东台富安中学九年级上学期学情调查数学卷 题型:解答题
(本题满分10分)已知函数y=mx2-6x+1(m是常数).
【小题1】⑴求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
【小题2】⑵若该函数的图象与x轴只有一个交点,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com