
科目: 来源:2011-2012年浙江省萧山城区九年级12月月考数学卷 题型:解答题
(12分)已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
【小题1】(1)求A、B、C三点的坐标;
【小题2】(2)求此抛物线的表达式;
【小题3】(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
【小题4】(4)在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2011-2012年浙江省萧山城区九年级12月月考数学卷 题型:解答题
(10分)有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类野生菌在冷库中最多保存160天,同时,平均每天有3千克的野生菌损坏不能出售。
【小题1】(1)设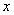 天后每千克该野生菌的市场价格为
天后每千克该野生菌的市场价格为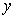 元,试写出
元,试写出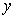 与
与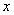 之间的函数关系式;
之间的函数关系式;
【小题2】(2)若存放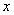 天后,将这批野生菌一次性出售,设这批野生菌的销售总额为
天后,将这批野生菌一次性出售,设这批野生菌的销售总额为 元,试写出
元,试写出 与
与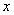 之间的函数关系式;
之间的函数关系式;
【小题3】(3)李经理将这批野生菌存放多少天后出售可获得最大利润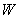 元?(利润=销售总额-收购成本-各种费用)
元?(利润=销售总额-收购成本-各种费用)
查看答案和解析>>
科目: 来源:2011-2012学年湖南省九年级上学期期末数学试卷 题型:解答题
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D
【小题1】求该抛物线的解析式与顶点D的坐标
【小题2】以B、C、D为顶点的三角形是直角三角形吗?为什么?
【小题3】探究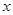 轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由
轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由
查看答案和解析>>
科目: 来源:2012届泰州市九年级期末模拟数学卷 题型:解答题
已知直角梯形纸片OABC在平面直角坐标系中的位置如图①所示,四
个顶点的坐标分别为O(0,0),A(10,0),B(8,2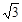 ),C(0,2
),C(0,2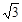 ),点P在线段OA上(不与O、A重合),将纸片折叠,使点A落在射线AB上(记为点A’),折痕PQ与射线AB交于点Q,设OP=x,折叠后纸片重叠部分的面积为y.(图②供探索用)
),点P在线段OA上(不与O、A重合),将纸片折叠,使点A落在射线AB上(记为点A’),折痕PQ与射线AB交于点Q,设OP=x,折叠后纸片重叠部分的面积为y.(图②供探索用)
【小题1】求∠OAB的度数;
【小题2】求y与x的函数关系式,并写出对应的x的取值范围;
【小题3】y存在最大值吗?若存在,求出这个最大值,并求此时x的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2012届泰州市九年级期末模拟数学卷 题型:解答题
)图①中是一座钢管混凝土系杆拱桥,桥的拱肋ACB可视为抛物线的一部分(如图②),桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,测得拱肋
的跨度AB为200米,与AB中点O相距20米处有一高度为48米的系杆.
【小题1】求正中间系杆OC的长度;
【小题2】若相邻系杆之间的间距均为5米(不考虑系杆的粗细),则是否存在一根系杆的长度恰好是OC长度的一半?请说明理由.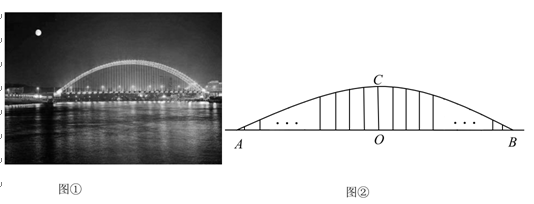
查看答案和解析>>
科目: 来源:2012届泰州市九年级期末模拟数学卷 题型:解答题
已知二次函数y=ax2+2x+c,函数y与自变量x的部分对应值如下表:
| x | …… | -2 | -1 | 0 | 1 | 2 | …… |
| y | …… | -5 | 0 | 3 | 4 | 3 | …… |
查看答案和解析>>
科目: 来源:2011-2012年北京市第六十六中学九年级上学期期中考试数学卷 题型:解答题
(本小题满分7分)如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,2OB=OD,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M.点P为线段FG上一个动点(与F、G不重合),
PQ∥y轴与抛物线交于点Q.
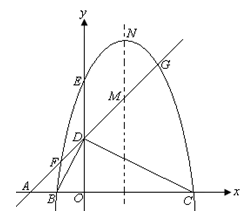 |
查看答案和解析>>
科目: 来源:2011-2012年北京市第六十六中学九年级上学期期中考试数学卷 题型:解答题
(本小题满分6分)在直角坐标平面中,O为坐标原点,二次函数 的图象与x轴的负半轴相交于点C(如图),点C的坐标为(0,-3),且BO=CO
的图象与x轴的负半轴相交于点C(如图),点C的坐标为(0,-3),且BO=CO
【小题1】(1)求这个二次函数的解析式;
【小题2】(2)设这个二次函数的图象的顶点为M,求AM 的长.
查看答案和解析>>
科目: 来源:2011-2012年北京市第六十六中学九年级上学期期中考试数学卷 题型:解答题
(本小题满分6分)某食品店零售店一种面包,统计销售情况发现,当这种面包的单价定为7角时,每天卖出160个.在此基础上,这种面包的单价每提高1角时,该零售店每天就会少卖出20个.考虑了所有因素后该零售店每个面包的成本是5角.设这种面包的单价为x(角),零售店每天销售这种面包所获得的利润为y(角).
【小题1】(1)用含x的代数式分别表示出每个面包的利润与卖出的面包个数;
【小题2】(2)求y与x之间的函数关系式及定义域;
【小题3】(3)当面包单价定为多少时,该零售店每天销售这种面包获得的利润最大?最大利润为多少?
查看答案和解析>>
科目: 来源:2011-2012年北京市第六十六中学九年级上学期期中考试数学卷 题型:解答题
(本小题满分5分)已知二次函数y= x2 +4x+3.
【小题1】(1)用配方法将y= x2 +4x+3化成y=a (x-h) 2 +k的形式,写出函数的最值;
【小题2】(2)在平面直角坐标系中,画出这个二次函数的图象;
【小题3】(3)写出当x为何值时,y>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com