
科目: 来源:2011-2012学年江苏省扬州市武坚中学九年级第一学期期末考试数学卷 题型:解答题
(本题满分12分)在直角坐标系中,抛物线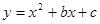 经过点(0,10)
经过点(0,10)
和点(4,2).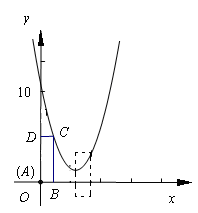
【小题1】(1) 求这条抛物线的函数关系式.
【小题2】(2)如图,在边长一定的矩形ABCD中,CD=1,点C在y轴右侧沿抛物线 滑动,在滑动过程中CD∥x轴,AB在CD的下方.当点D在y轴上时,AB正好落在x轴上.
滑动,在滑动过程中CD∥x轴,AB在CD的下方.当点D在y轴上时,AB正好落在x轴上.
①求边BC的长.
②当矩形ABCD在滑动过程中被x轴分成两部分的面
积比为1:4时,求点C的坐标.
查看答案和解析>>
科目: 来源:2011-2012学年江苏省扬州市武坚中学九年级第一学期期末考试数学卷 题型:解答题
(本题满分10分)
为了保证春节期间的水果供应,保障水果的无公害,江都“乐天玛特”超市从水果原产地联系了一种水果,根据以往销售经验,估计春节期间,这种水果每天的单价x元与销售量y千克之间有如下的一次函数的关系:
| 每千克的 售价(元) | 41 | 40 | 39 | 38 | …… |
| 每天的销售量(千克) | 50 | 55 | 60 | 65 | …… |
查看答案和解析>>
科目: 来源:2012届江苏省苏州市工业园区九年级上学期期末调研数学卷 题型:解答题
(本题满分10分)如图1,点C、B分别为抛物线C1:y1=x2+1,抛物线C2:y2=a2x2+b2x+c2的顶点.分别过点B、C作x轴的平行线,交抛物线C1、C2于点A、D,且AB=BD.
【小题1】(1)求点A的坐标:
【小题2】(2)如图2,若将抛物线C1:“y1=x2+1”改为抛物线“y1=2x2+b1x+c1”.其他条件不变,求CD的长和a2的值;
【小题3】(3)如图2,若将抛物线C1:“y1=x2+1”改 为抛物线“y1=4x2+b1x+c1”,其他条件不变,求b1+b2的值 ▲ (直接写结果).
为抛物线“y1=4x2+b1x+c1”,其他条件不变,求b1+b2的值 ▲ (直接写结果).
查看答案和解析>>
科目: 来源:2012届江苏省苏州市工业园区九年级上学期期末调研数学卷 题型:解答题
( 本题满分8分)已知抛物线y=x2+(b-1)x+c经过点P(-1,-2b),
本题满分8分)已知抛物线y=x2+(b-1)x+c经过点P(-1,-2b),
【小题1】(1)求b+c的值;
【小题2】 (2)若b=3,求这条抛物线的顶点坐标;
【小题3】(3)若b>3,过点P作直线PA⊥y轴,交y轴于点A,交抛物线于另一点B,且BP=2PA,求这条抛物线所对应的二次函数关系式.
查看答案和解析>>
科目: 来源:2012届北京市密云县九年级第一学期期末考试数学卷 题型:解答题
在平面直角坐标系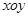 中,以点A(3,0)为圆心,5为半径的圆与
中,以点A(3,0)为圆心,5为半径的圆与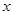 轴相交于点
轴相交于点 、
、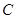 (点B在点C的左边),与
(点B在点C的左边),与 轴相交于点D、M(点D在点M的下方).
轴相交于点D、M(点D在点M的下方).
【小题1】(1)求以直线x=3为对称轴,且经过D、C两点的抛物线的解析式;
【小题2】(2)若E为直线x=3上的任一点,则在抛物线上是否存在
这样的点F,使得以点B、C、E、F为顶点的四边形是平
行四边形?若存在,求出点F的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2012届北京市密云县九年级第一学期期末考试数学卷 题型:解答题
已知二次函数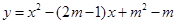 (
( 是常数,且
是常数,且 ).
).
【小题1】(1)证明:不论m取何值时,该二次函数图象总与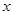 轴有两个交点;
轴有两个交点;
【小题2】(2)设与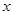 轴两个交点的横坐标分别为
轴两个交点的横坐标分别为 ,
, (其中
(其中 >
> ),若
),若 是关于
是关于 的函数,且
的函数,且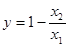 ,结合函数的图象回答:当自变量m的取值满足什么条件时,
,结合函数的图象回答:当自变量m的取值满足什么条件时, ≤2.
≤2.
查看答案和解析>>
科目: 来源:2012届北京市密云县九年级第一学期期末考试数学卷 题型:解答题
密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.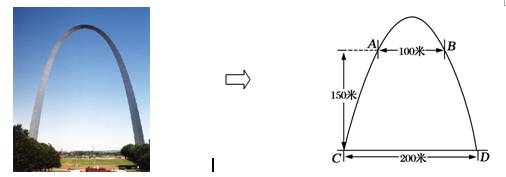
查看答案和解析>>
科目: 来源:2012届北京市密云县九年级第一学期期末考试数学卷 题型:解答题
用配方法将二次函数 化为
化为 的形式(其中
的形式(其中 为常数
为常数 ),写出这个二次函数图象的顶点坐标 和对称轴方程,并在直角坐标系中画出他的示意图.
),写出这个二次函数图象的顶点坐标 和对称轴方程,并在直角坐标系中画出他的示意图.
查看答案和解析>>
科目: 来源:2012届北京市怀柔区茶坞铁路学校九年级上学期期末考试数学卷 题型:解答题
已知抛物线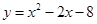 .
.
【小题1】(1)用配方法把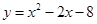 化为
化为 形式;
形式;
【小题2】(2)并指出:抛物线的顶点坐标是 ,抛物线的对称轴方程是 ,
抛物线与x轴交点坐标是 ,当x 时,y随x的增大而增大.
解
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com