
科目: 来源:2011-2012年北京市三帆中学九年级上学期期中测试数学卷 题型:解答题
已知二次函数y=x2-(2a+3)x+4a+2与x轴交于A、B两点,与y轴交于点C,并且点A在点B左侧,位于原点两侧. 若S△ABC的面积为3,求a的值.
查看答案和解析>>
科目: 来源:2011-2012年北京市三帆中学九年级上学期期中测试数学卷 题型:解答题
某数码卖场销售某种品牌电脑,对于100~500台的大客户订单实行降价促销,每台电脑的售价y(元/台)与数量x(台)的函数关系可以由图中线段AB来表示,每台电脑的进货及运输等成本总共为2250元。
【小题1】(1)写出每台电脑的售价y与台数x的函数关系式:________________;自变量的取值范围是____________且x为整数;
【小题2】(2)若一次政府采购的订单使该卖场共获利12万元,不计其它成本消耗,试求出这次政府采购了多少台电脑;
【小题3】(3)求出每份大客户订单的总获利z(元)与购买数量x(台)之间的函数关系式。当一份订单的购买数量为多少台时,卖场获利最多?
查看答案和解析>>
科目: 来源:2011-2012年北京市三帆中学九年级上学期期中测试数学卷 题型:解答题
已知二次函数y=ax2+bx+c(a≠0)的图象过点A(2,0),B(-2,-4),对称轴为直线x=-1. 【小题1】(1)求这个二次函数的解析式;【小题2】(2)若-3<x<3,直接写出y的取值范围;【小题3】(3)若一元二次方程ax2+bx+c-m=0(a≠0,m为实数)在-3<x<3的范围内有实数根,直接写出m的取值范围.
查看答案和解析>>
科目: 来源:2011-2012年北京市三帆中学九年级上学期期中测试数学卷 题型:解答题
对于抛物线y=x2-4x+3,
【小题1】(1)与y轴的交点坐标是___________,与x轴的交点坐标是_______________,
顶点坐标是____________.
【小题2】(2)在坐标系中利用描点法画出此抛物线.
| x | ... | | | | | | ... |
| y | ... | | | | | | ... |
查看答案和解析>>
科目: 来源:2012届北京市延庆县九年级上学期期末考试数学卷 题型:解答题
已知二次函数 的图象与x轴交于点A(4,0)、点B,与y轴交于
的图象与x轴交于点A(4,0)、点B,与y轴交于 点C。
点C。
【小题1】(1)求此二次函数的解析式及点B的坐标;
【小题2】(2)点P从点A出发以每秒1个单位的速度沿线段AO向O点运动,到达点O后停止运动,过点P作PQ//AC交OC于点Q,将四边形PQCA沿PQ翻折,得到四边形 ,设点P的运动时间为t。
,设点P的运动时间为t。
①当t为何值时,点 恰好落在二次函数
恰好落在二次函数 的图象的对称轴上;
的图象的对称轴上;
②设四边形 落在第一象限内的图形面积为S,求S关于t的函数关系式,并求出当t为何值时S的值最大。
落在第一象限内的图形面积为S,求S关于t的函数关系式,并求出当t为何值时S的值最大。
查看答案和解析>>
科目: 来源:2012届北京市延庆县九年级上学期期末考试数学卷 题型:解答题
已知关于x的一元二次方程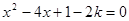 有两个不等的实根,
有两个不等的实根,
【小题1】(1)求k的取值范围;
【小题2】(2)若k取小于1的整数,且此方程的解为整数,则求出此方程的两个整数根;
【小题3】(3)在(2)的条件下,二次函数 与x轴交于A、B两点(A点在B点的左侧),D点在此抛物线的对称轴上,若
与x轴交于A、B两点(A点在B点的左侧),D点在此抛物线的对称轴上,若 ,求D点的坐标。
,求D点的坐标。
查看答案和解析>>
科目: 来源:2012届北京市延庆县九年级上学期期末考试数学卷 题型:解答题
已知二次函数y= x2 +4x+3.
【小题1】(1)用配方法将y= x2 +4x+3化成y=a (x-h) 2 +k的形式;
【小题2】(2)在平面直角坐标系中,画出这个二次函数的图象;
【小题3】(3)写出当x为何值时,y>0.
查看答案和解析>>
科目: 来源:2011-2012年北京教育学院附属中学九年级第一学期期中测试数学卷 题型:解答题
已知抛物线y=x2+kx+k-2.
【小题1】(1)求证:不论k为任何实数,抛物线与x轴总有两个交点;
【小题2】(2)若反比例函数 的图象与
的图象与 的图象关于y轴对称,又与抛物线交于点A(n,-3),求抛物线的解析式;
的图象关于y轴对称,又与抛物线交于点A(n,-3),求抛物线的解析式;
【小题3】(3)若点P是(2)中抛物线上的一点,且点P到两坐标轴的距离相等,求点P的坐标.
查看答案和解析>>
科目: 来源:2011-2012年北京教育学院附属中学九年级第一学期期中测试数学卷 题型:解答题
已知抛物线C1: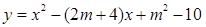 的顶点A到
的顶点A到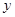 轴的距离为3, 与
轴的距离为3, 与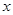 轴交于C、D两点.
轴交于C、D两点.
【小题1】(1)求顶点A的坐标;
【小题2】(2)若点B在抛物线C1上,且 ,求点B的坐标.
,求点B的坐标.
查看答案和解析>>
科目: 来源:2011-2012年北京教育学院附属中学九年级第一学期期中测试数学卷 题型:解答题
某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: .
.
【小题1】(1)设李明每月获得利润为w(元)(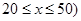 ,当销售单价定为多少元时,每月可获得最大利润?
,当销售单价定为多少元时,每月可获得最大利润?
【小题2】(2)如果李明想要每月获得2000元的利润,并且又要减少库存,那么销售单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com